- 【割合1】何倍になっているかで比べるプリント数:4
- 【割合2】割合を求めようプリント数:16
- 【割合3】色々なもとにする量の割合を求めようプリント数:4
- 【割合4】割合を百分率で表そうプリント数:16
- 【割合5】百分率を小数で表そうプリント数:16
- 【割合6】割合を歩合で表そうプリント数:16
- 【割合7】歩合を小数で表そうプリント数:16
- 【割合8】もとにする量・比べられる量・割合を見分けるプリント数:16
- 【割合9】割合(何%か)を求めるプリント数:16
- 【割合10】比べられる量を求めるプリント数:16
- 【割合11】もとにする量を求めるプリント数:16
- 【割合12】割引きされた代金を求めるプリント数:16
- 【割合13】利益を加えた売値を求めるプリント数:16
- 【割合14】割引きについて考えようプリント数:16
【割合1】何倍になっているかで比べる

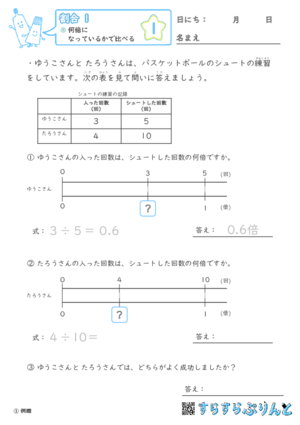
二人でバスケットボールのシュート練習をしています。「入った回数はシュートした回数の何倍ですか」という問題と「どちらがよく成功しましたか」とういう成功率のより高い人物を答える問題を集めた学習プリントです。
入った数は、シュートした回数より必ず少なくなります。
入った数とシュートした数が同じであれば「1倍」という答えになります。
このことが、ヒントとしてついている比例数直線でよくわかると思います。
式は【入った数÷シュートした数】でたてて、答えは「0.いくつ」の1より小さい小数点のついた数字になりますよ。
どちらがよく成功したか? は、この数字が高い方(1に近い方)ということになります。
図でも、シュートが全部成功した場合の1倍に対して、どの程度の成功率だったかを目視できるようにしてあります。
このプリントでは二人の成功率をどちらも図にしてあるので、【?】のついたそれぞれの成功率のラインを縦に見比べることでも、感覚的に答えを知ることができます。
この図が何をあらわしているか? しっかり理解することが割合を理解するためのステップになりますよ!
「【割合1】何倍になっているかで比べる」プリント一覧
リンクをクリックするとPDFが表示されます。
【割合2】割合を求めよう

割合の公式を確認して、いろいろな割合を求める問題を集めた学習プリントです。
最初は、【割合1】何倍になっているかで比べるでやった「シュートの回数と入った回数」なので、式の立て方も一緒でわかりやすいと思います。
ここで、割合の公式と【比べられる量】と【もとにする量】という用語が出てきます。
もとにする量を1として、比べられる量が少ない場合は、1以下の小数になります。
割合=比べられる数÷もとにする量
という公式を『例題』と『確認』で覚えてしまいましょう!
【割合とは比べられる量が、もとにする量の何倍になるかをあらわした数を「割合」といいます】という言葉の定義もあわせてのせてあります。
言葉の定義は音読をするのも良いですね。
『定着』からは問題数が増えます。
『仕上げ』からは比例数直線がなくなり、計算スペースがあります。
割り算の筆算に使ってください。
「【割合2】割合を求めよう」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】割合を求めよう【割合2】01例題
- 【02】割合を求めよう【割合2】02確認
- 【03】割合を求めよう【割合2】03確認
- 【04】割合を求めよう【割合2】04確認
- 【05】割合を求めよう【割合2】05定着
- 【06】割合を求めよう【割合2】06定着
- 【07】割合を求めよう【割合2】07定着
- 【08】割合を求めよう【割合2】08定着
- 【09】割合を求めよう【割合2】09定着
- 【10】割合を求めよう【割合2】10仕上げ
- 【11】割合を求めよう【割合2】11仕上げ
- 【12】割合を求めよう【割合2】12仕上げ
- 【13】割合を求めよう【割合2】13仕上げ
- 【14】割合を求めよう【割合2】14仕上げ
- 【15】割合を求めよう【割合2】15力だめし
- 【16】割合を求めよう【割合2】16力だめし
【割合3】色々なもとにする量の割合を求めよう

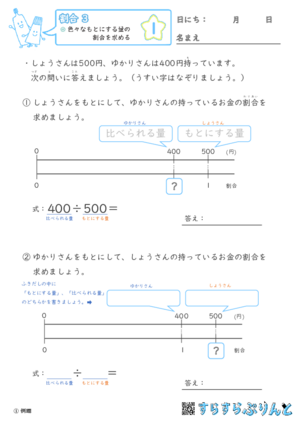
Aさんはいくら、Bさんはいくら持っています。AさんをもとにしてBさんの持っているお金の割合は? という問題と、その逆(BさんをもとにしてAさんのもっているお金)の問題を集めた学習プリントです。
【Aさんをもとにして】という問題ではAさんが「もとにする量」で、Bさんが「比べられる量」です。
逆にした場合は【Bさんをもとにして】と書いてあるので、Bさんが「もとにする量」でAさんが「比べられる量」になりますね。
まずは比例数直線になっている図に、「もとにする量」と「比べられる量」を、どちらがどちらか書き込んでみましょう!
『例題』では、式のところに【比べられる量÷もとにする量】ということが、わかるように書いてあります。
比例数直線の空欄に書き込む言葉を正しくかければ、式を正しくかけるというわけです。
『確認』の途中からこのヒントがなくなりますが、同じように考えて式をたててみましょう。
割合は、どちらを元にするか? によって、大きい方をもとにした場合は1より小さく、小さい方をもとにした場合は1より大きくなります。
ふたつ並んでいることで、この性質にも気づくきっかけになるかもしれませんね。
「【割合3】色々なもとにする量の割合を求めよう」プリント一覧
リンクをクリックするとPDFが表示されます。
【割合4】割合を百分率で表そう

割合から百分率への変換をする問題を集めた学習プリントです。
『例題』と『確認』では、百分率の定義と「%」の書き方のなぞりもあります。
【割合は%(%)で表すこともできます。%で表した割合を百分率といいます。割合の1は100%です。】という言葉の定義は、音読して覚えてしまうといいですね!
また割合を表す数字と、百分率の対応表の問題と、「次の割合を百分率で表しましょう」といういろいろな割合(0.007等も!)が出てくる問題があります。
このすらぷりでしっかり練習して、割合を百分率で言い換えられるようになりましょう。
1→100%
0.1→10%
0.01→1%
0.001→0.1%
まずはこの変換をすらすら出来るようになるところがスタートですよ!
『仕上げ』と『力だめし』では割合を求める問題が混ぜてあります。
「【割合4】割合を百分率で表そう」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】割合を百分率で表そう【割合4】01例題
- 【02】割合を百分率で表そう【割合4】02確認
- 【03】割合を百分率で表そう【割合4】03確認
- 【04】割合を百分率で表そう【割合4】04確認
- 【05】割合を百分率で表そう【割合4】05定着
- 【06】割合を百分率で表そう【割合4】06定着
- 【07】割合を百分率で表そう【割合4】07定着
- 【08】割合を百分率で表そう【割合4】08定着
- 【09】割合を百分率で表そう【割合4】09定着
- 【10】割合を百分率で表そう【割合4】10仕上げ
- 【11】割合を百分率で表そう【割合4】11仕上げ
- 【12】割合を百分率で表そう【割合4】12仕上げ
- 【13】割合を百分率で表そう【割合4】13仕上げ
- 【14】割合を百分率で表そう【割合4】14仕上げ
- 【15】割合を百分率で表そう【割合4】15力だめし
- 【16】割合を百分率で表そう【割合4】16力だめし
【割合5】百分率を小数で表そう

割合について、百分率(%)で表したものを、小数に変換する問題を集めた学習プリントです。
『例題』から『定着』まで、100%・10%・1%・0.1%がそれぞれ割合を表す数(小数)ではどう表されるかをまとめる表の問題がついています。
100%→1
10%→0.1
1%→0.01
0.1%→0.001
ということですね。
またメインの問題として、さまざまな百分率(%)を小数に変換する問題をたくさん用意してあります。
120%のように100%を超えていたり(1.2になりますよ!)
10.5%のように百分率の方に小数点がついてたりします。(0.105になります。間の0もなくならないように注意!)
自分の間違いやすいパターンをみつけたら、気を付けて取り組むようにしましょうね。
『仕上げ』と『力だめし』では、割合(小数)を百分率になおす問題を混ぜてあります。
「【割合5】百分率を小数で表そう」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】百分率を小数で表そう【割合5】01例題
- 【02】百分率を小数で表そう【割合5】02確認
- 【03】百分率を小数で表そう【割合5】03確認
- 【04】百分率を小数で表そう【割合5】04確認
- 【05】百分率を小数で表そう【割合5】05定着
- 【06】百分率を小数で表そう【割合5】06定着
- 【07】百分率を小数で表そう【割合5】07定着
- 【08】百分率を小数で表そう【割合5】08定着
- 【09】百分率を小数で表そう【割合5】09定着
- 【10】百分率を小数で表そう【割合5】10仕上げ
- 【11】百分率を小数で表そう【割合5】11仕上げ
- 【12】百分率を小数で表そう【割合5】12仕上げ
- 【13】百分率を小数で表そう【割合5】13仕上げ
- 【14】百分率を小数で表そう【割合5】14仕上げ
- 【15】百分率を小数で表そう【割合5】15力だめし
- 【16】百分率を小数で表そう【割合5】16力だめし
【割合6】割合を歩合で表そう

割合を歩合で表す問題を集めた学習プリントです。
『例題』から『定着』まで対応表を埋める問題がついています。
| 割合を表す数 | 1 | 0.1 | 0.01 | 0.001 |
|---|---|---|---|---|
| 百分率 | 100% | 10% | 1% | 0.1% |
| 歩合 | 10割 | 1割 | 1分 | 1厘 |
この表がわかれば、割合を歩合であらわせるようになります。
すらぷりでは、なぞりから練習するので不安な生徒さんも大丈夫。
歩合は、野球の打率などで使う言葉でもありますね。
6割4分7厘など、歩合は単位を組み合わせて使うことも知って、使いこなしていきましょう!
『仕上げ』と『力だめし』では割合を小数で表す問題も混ぜてあります。
「【割合6】割合を歩合で表そう」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】割合を歩合で表そう【割合6】01例題
- 【02】割合を歩合で表そう【割合6】02確認
- 【03】割合を歩合で表そう【割合6】03確認
- 【04】割合を歩合で表そう【割合6】04確認
- 【05】割合を歩合で表そう【割合6】05定着
- 【06】割合を歩合で表そう【割合6】06定着
- 【07】割合を歩合で表そう【割合6】07定着
- 【08】割合を歩合で表そう【割合6】08定着
- 【09】割合を歩合で表そう【割合6】09定着
- 【10】割合を歩合で表そう【割合6】10仕上げ
- 【11】割合を歩合で表そう【割合6】11仕上げ
- 【12】割合を歩合で表そう【割合6】12仕上げ
- 【13】割合を歩合で表そう【割合6】13仕上げ
- 【14】割合を歩合で表そう【割合6】14仕上げ
- 【15】割合を歩合で表そう【割合6】15力だめし
- 【16】割合を歩合で表そう【割合6】16力だめし
【割合7】歩合を小数で表そう

歩合で表した割合を小数で表す問題を集めた学習プリントです。
『例題』と『定着』までは、前回と同じように対応がわか表がついています。
メインの問題は、
4割→0.4
7割5分→0.75
3厘→0.003
2割1分→0.21
5割2分4厘→0.524
といったように、いろいろなバリエーションを問われます。
また『仕上げ』と『力だめし』では小数であらわされた割合を歩合で表す問題も混ぜてあります。
「【割合7】歩合を小数で表そう」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】歩合を小数で表そう【割合7】01例題
- 【02】歩合を小数で表そう【割合7】02確認
- 【03】歩合を小数で表そう【割合7】03確認
- 【04】歩合を小数で表そう【割合7】04確認
- 【05】歩合を小数で表そう【割合7】05定着
- 【06】歩合を小数で表そう【割合7】06定着
- 【07】歩合を小数で表そう【割合7】07定着
- 【08】歩合を小数で表そう【割合7】08定着
- 【09】歩合を小数で表そう【割合7】09定着
- 【10】歩合を小数で表そう【割合7】10仕上げ
- 【11】歩合を小数で表そう【割合7】11仕上げ
- 【12】歩合を小数で表そう【割合7】12仕上げ
- 【13】歩合を小数で表そう【割合7】13仕上げ
- 【14】歩合を小数で表そう【割合7】14仕上げ
- 【15】歩合を小数で表そう【割合7】15力だめし
- 【16】歩合を小数で表そう【割合7】16力だめし
【割合8】もとにする量・比べられる量・割合を見分ける

文章をみて、「もとにする量」「比べられる量」「割合」がそれぞれ何か答える問題を集めた学習プリントです。
例えば「100cmの30%は30cmです」という文章では、
もとにする量・・・100cm
比べられる量・・・30cm
割合・・・・・・・30%
となります。
言葉の語順などは毎回かわりますから、どんな文章が出てきても図でイメージすることが大事です。
どんな図をイメージしたらいいかは、『例題』で書いてありますよ。
比例数直線は、イメージした図をさらに模式的にあらわしたものです。
上に具体物・下に割合の数直線があります。
100%と対応する上の数直線に「もとにする量」
問題文の「割合」と対応する上の数直線に「比べられる量」を書きます。
また、【割合=比べられる量÷もとにする量】という公式も、このプリントで確認できます。
『定着』では、「く・も・わ」の図で割合の公式を覚える方法も解説しています。
『仕上げ』と『力だめし』では、割合を小数や百分率であらわす問題を混ぜてあります。
割合の文章問題では、問題文の中から「もとにする量」「比べられる量」「割合」を見分けることがまず第一歩!
つまづきの原因に気づいて学習することができますし、割合の基礎の総チェックとして力がついたか確認することもできますね。
「【割合8】もとにする量・比べられる量・割合を見分ける」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】もとにする量・比べられる量・割合を見分ける【割合8】01例題
- 【02】もとにする量・比べられる量・割合を見分ける【割合8】02確認
- 【03】もとにする量・比べられる量・割合を見分ける【割合8】03確認
- 【04】もとにする量・比べられる量・割合を見分ける【割合8】04確認
- 【05】もとにする量・比べられる量・割合を見分ける【割合8】05定着
- 【06】もとにする量・比べられる量・割合を見分ける【割合8】06定着
- 【07】もとにする量・比べられる量・割合を見分ける【割合8】07定着
- 【08】もとにする量・比べられる量・割合を見分ける【割合8】08定着
- 【09】もとにする量・比べられる量・割合を見分ける【割合8】09定着
- 【10】もとにする量・比べられる量・割合を見分ける【割合8】10仕上げ
- 【11】もとにする量・比べられる量・割合を見分ける【割合8】11仕上げ
- 【12】もとにする量・比べられる量・割合を見分ける【割合8】12仕上げ
- 【13】もとにする量・比べられる量・割合を見分ける【割合8】13仕上げ
- 【14】もとにする量・比べられる量・割合を見分ける【割合8】14仕上げ
- 【15】もとにする量・比べられる量・割合を見分ける【割合8】15力だめし
- 【16】もとにする量・比べられる量・割合を見分ける【割合8】16力だめし
【割合9】割合(何%か)を求める

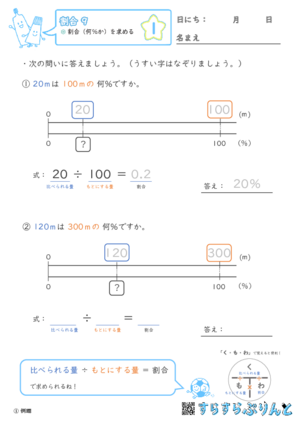
百分率で答える割合の文章問題、つまり「□□は 〇〇の 何%ですか」という問題等を集めた学習プリントです。
出てくる答えは割合の小数ですから、そこから百分率に変換して答えにかくことがポイントですよ!
『例題』『確認』では、比例数直線&色で「比べられる量」「もとにする量」を示したヒント&ページ下に公式と「く・も・わ」……と、ヒント盛沢山です。
ですから、最初の4枚ははカラー印刷がオススメです。
『定着』『仕上げ』からは、ヒントはなしで、計算スペースがつけてあります。
自分で筆算をしましょう。
ここからは、ペットボトルや本など具体例を用いた文章題も出てきます。
「比べられる量」と「もとにする量」が文章の中のどれか、比例数直線を描いたりイメージしながら探すのもいいですね。
100%に対応する量はどれか……と考えると、「もとにする量」がみつかりますよ。
『力だめし』は、配点の関係で2問です。
「【割合9】割合(何%か)を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】割合(何%か)を求める【割合9】01例題
- 【02】割合(何%か)を求める【割合9】02確認
- 【03】割合(何%か)を求める【割合9】03確認
- 【04】割合(何%か)を求める【割合9】04確認
- 【05】割合(何%か)を求める【割合9】05定着
- 【06】割合(何%か)を求める【割合9】06定着
- 【07】割合(何%か)を求める【割合9】07定着
- 【08】割合(何%か)を求める【割合9】08定着
- 【09】割合(何%か)を求める【割合9】09定着
- 【10】割合(何%か)を求める【割合9】10仕上げ
- 【11】割合(何%か)を求める【割合9】11仕上げ
- 【12】割合(何%か)を求める【割合9】12仕上げ
- 【13】割合(何%か)を求める【割合9】13仕上げ
- 【14】割合(何%か)を求める【割合9】14仕上げ
- 【15】割合(何%か)を求める【割合9】15力だめし
- 【16】割合(何%か)を求める【割合9】16力だめし
【割合10】比べられる量を求める

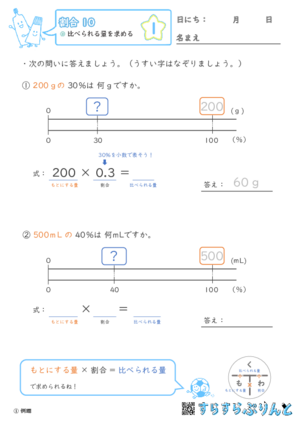
「200gの30%は何gですか」等、比べられる量を求める文章題を集めた学習プリントです。
『例題』『確認』はヒント多めでやり方の解説になっています。
●「比べられる量」は、「もとにする量」×「割合」で求める
●「割合」は、問題文が百分率でも小数であらわすこと
ということが、『例題』『確認』の解説でわかります。
ヒントはカラーなので最初の4セットはカラー印刷がおすすめです。
『定着』と『仕上げ』では、シンプルな1行問題だけではなく、本やシュート率など具体的な状況が書かれた文章題も出てきます。
その文章が「比べられる量」を聞かれている問題であることを意識しながら、「もとにする量」と「割合」をチェックして式をたてましょう。
『力だめし』は配点の関係で2問になります。
「【割合10】比べられる量を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】比べられる量を求める【割合10】01例題
- 【02】比べられる量を求める【割合10】02確認
- 【03】比べられる量を求める【割合10】03確認
- 【04】比べられる量を求める【割合10】04確認
- 【05】比べられる量を求める【割合10】05定着
- 【06】比べられる量を求める【割合10】06定着
- 【07】比べられる量を求める【割合10】07定着
- 【08】比べられる量を求める【割合10】08定着
- 【09】比べられる量を求める【割合10】09定着
- 【10】比べられる量を求める【割合10】10仕上げ
- 【11】比べられる量を求める【割合10】11仕上げ
- 【12】比べられる量を求める【割合10】12仕上げ
- 【13】比べられる量を求める【割合10】13仕上げ
- 【14】比べられる量を求める【割合10】14仕上げ
- 【15】比べられる量を求める【割合10】15力だめし
- 【16】比べられる量を求める【割合10】16力だめし
【割合11】もとにする量を求める

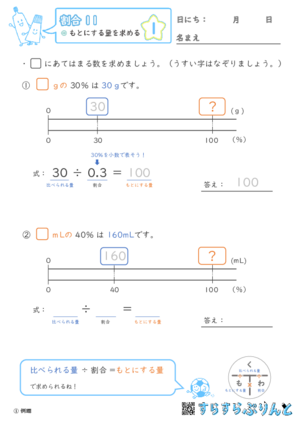
「□gの30%は30gです」(□に当てはまる数を求めましょう)等、もとにする量を求める文章題を集めた学習プリントです。
●「もとにする量」は、「比べられる量」÷「割合」で求める。
●割合は小数で!
というポイントは一貫しているので、今までのプリントで比例数直線や「く・も・わ」に慣れてきた生徒さんであれば、ピンときやすいと思います。
『確認』の最後(4枚目)からは、「バスに10人乗っています。これは、バスの定員の20%にあたります。このバスの定員は何人ですか」といったような、文章の問題も出てきます。
また『仕上げ』からは、比べられる量を求める問題も混ぜてあります。
問題が混ざってくるといっそう、「もとにする量」「比べられる量」「割合」の見分けが大切になってきますね。
【割合8】もとにする量・比べられる量・割合を見分けるプリントも活用して、文章を読み解く力をつけていきましょう。
「【割合11】もとにする量を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】もとにする量を求める【割合11】01例題
- 【02】もとにする量を求める【割合11】02確認
- 【03】もとにする量を求める【割合11】03確認
- 【04】もとにする量を求める【割合11】04確認
- 【05】もとにする量を求める【割合11】05定着
- 【06】もとにする量を求める【割合11】06定着
- 【07】もとにする量を求める【割合11】07定着
- 【08】もとにする量を求める【割合11】08定着
- 【09】もとにする量を求める【割合11】09定着
- 【10】もとにする量を求める【割合11】10仕上げ
- 【11】もとにする量を求める【割合11】11仕上げ
- 【12】もとにする量を求める【割合11】12仕上げ
- 【13】もとにする量を求める【割合11】13仕上げ
- 【14】もとにする量を求める【割合11】14仕上げ
- 【15】もとにする量を求める【割合11】15力だめし
- 【16】もとにする量を求める【割合11】16力だめし
【割合12】割引きされた代金を求める

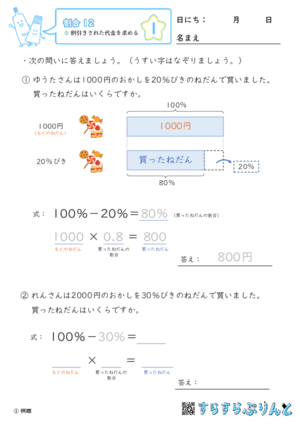
「□円のおかしを20%引きの値段でかいました。買った値段はいくらですか」という問題を集めた学習プリントです。
実際、お店でもよくみる【〇%引き】の表記。
買った値段は、「100%-〇%」で出します。
20%引きなら、80%の値段が買った値段ですね。
そこから「□円(もとの値段)×0.8(買った値段の割合)」という式を立てて、買った値段を出します。
2段階で求める問題なので、最初は少し難しく感じるかもしれませんが、日常に密着した算数なので、是非マスターしましょう。
『例題』『確認』までは解説&ヒントが多め。
『定着』『仕上げ』では問題数が3問。
逆に『力だめし』では配点の都合で2問になっています。
ヒントをしっかり見るなら、5枚目まではカラーがおすすめです。
「【割合12】割引きされた代金を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】割引きされた代金を求める【割合12】01例題
- 【02】割引きされた代金を求める【割合12】02確認
- 【03】割引きされた代金を求める【割合12】03確認
- 【04】割引きされた代金を求める【割合12】04確認
- 【05】割引きされた代金を求める【割合12】05定着
- 【06】割引きされた代金を求める【割合12】06定着
- 【07】割引きされた代金を求める【割合12】07定着
- 【08】割引きされた代金を求める【割合12】08定着
- 【09】割引きされた代金を求める【割合12】09定着
- 【10】割引きされた代金を求める【割合12】10仕上げ
- 【11】割引きされた代金を求める【割合12】11仕上げ
- 【12】割引きされた代金を求める【割合12】12仕上げ
- 【13】割引きされた代金を求める【割合12】13仕上げ
- 【14】割引きされた代金を求める【割合12】14仕上げ
- 【15】割引きされた代金を求める【割合12】15力だめし
- 【16】割引きされた代金を求める【割合12】16力だめし
【割合13】利益を加えた売値を求める

「あるゲームを□円で仕入れました。利益を30%加えて売るとき、売る値段はいくらになりますか」という問題を集めた学習プリントです。
仕入れた値段が「もとの値段」で、うる値段をもとめます。
100%の値段に30%上乗せしているわけですから、求める値段は130%(100+30で求めます)
そこから、「□円(もとの値段)×1.3(売る値段の割合)」という式をたてて答えを出します。
『例題』『確認』は問題数をおさえてヒントがしっかりめ。
『定着』の7までが、式をたてるところにヒントが書いてあります。(いちおうカラー)
『仕上げ』でも集中して利益を加えた売値の問題だけになっています。
『力だめし』は、配点の都合もあり2問です。
「【割合13】利益を加えた売値を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】利益を加えた売値を求める【割合13】01例題
- 【02】利益を加えた売値を求める【割合13】02確認
- 【03】利益を加えた売値を求める【割合13】03確認
- 【04】利益を加えた売値を求める【割合13】04確認
- 【05】利益を加えた売値を求める【割合13】05定着
- 【06】利益を加えた売値を求める【割合13】06定着
- 【07】利益を加えた売値を求める【割合13】07定着
- 【08】利益を加えた売値を求める【割合13】08定着
- 【09】利益を加えた売値を求める【割合13】09定着
- 【10】利益を加えた売値を求める【割合13】10仕上げ
- 【11】利益を加えた売値を求める【割合13】11仕上げ
- 【12】利益を加えた売値を求める【割合13】12仕上げ
- 【13】利益を加えた売値を求める【割合13】13仕上げ
- 【14】利益を加えた売値を求める【割合13】14仕上げ
- 【15】利益を加えた売値を求める【割合13】15力だめし
- 【16】利益を加えた売値を求める【割合13】16力だめし
【割合14】割引きについて考えよう

「あるスーパーでは、木曜日と金曜日が特売日です。木曜日は魚が2割引きで買えます。金曜日は魚が50円引きになります。」とうような条件で、木曜日のサンマとアジの値段を考えたり、木曜日と金曜日でサンマの値段はどちらが安いか考える問題を集めた学習プリントです。
木曜日のサンマとアジの値段を求めるのは、【割合12】割引きされた代金を求めるでやった方法とほとんど同じですね。
ここでは百分率を使った問題文ではないので、「1-0.2=0.8」という形で、買った値段の割合を出しています。
曜日ごとの値段を比べるには、【何割引き】の日の値段を計算して調べてから、【〇円引き】の日の値段も出して比べます。
楽な道はありませんね!
『仕上げ』と『力だめし』では、「〇曜日の方が□円安い」で答える問題に絞って出してあります。
ものの値段が違えば、お得な曜日が違ってくることもあるのが面白いところ。
最初は少し難しく感じるかもしれませんが、日常生活でもよく使う割合の考え方なので、是非マスターしましょう。
「【割合14】割引きについて考えよう」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】割引きについて考えよう【割合14】01例題
- 【02】割引きについて考えよう【割合14】02確認
- 【03】割引きについて考えよう【割合14】03確認
- 【04】割引きについて考えよう【割合14】04確認
- 【05】割引きについて考えよう【割合14】05定着
- 【06】割引きについて考えよう【割合14】06定着
- 【07】割引きについて考えよう【割合14】07定着
- 【08】割引きについて考えよう【割合14】08定着
- 【09】割引きについて考えよう【割合14】09定着
- 【10】割引きについて考えよう【割合14】10仕上げ
- 【11】割引きについて考えよう【割合14】11仕上げ
- 【12】割引きについて考えよう【割合14】12仕上げ
- 【13】割引きについて考えよう【割合14】13仕上げ
- 【14】割引きについて考えよう【割合14】14仕上げ
- 【15】割引きについて考えよう【割合14】15力だめし
- 【16】割引きについて考えよう【割合14】16力だめし