- 【対称な図形1】二等辺三角形と線対称プリント数:2
- 【対称な図形2】線対称の軸プリント数:16
- 【対称な図形3】線対称な図形の対応する点プリント数:16
- 【対称な図形4】線対称な図形の軸プリント数:4
- 【対称な図形5】線対称な図形の作図(マス目あり)プリント数:16
- 【対称な図形6】線対称な図形の作図(マス目なし)プリント数:16
- 【対称な図形7】点対称な図形の重なり方プリント数:4
- 【対称な図形8】点対称な図形を見つけるプリント数:16
【対称な図形1】二等辺三角形と線対称

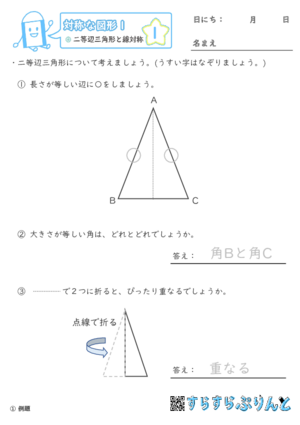
二等辺三角形の長さが等しい辺を選ぶ問題と、点線で二等辺三角形を二つに折ったときぴったり重なるかどうかを考える問題の学習プリントです。
見た目の異なる二つの二等辺三角形の問題を用意しました。
二等辺三角形の同じ長さの辺を見つけるのは、見た目でピンとこなければ、定規やコンパスで測ってみましょう。
長さが同じ辺の間の頂点から底辺に対して垂直に伸ばした直線は、二等辺三角形の線対称の軸になります。
この直線で二等辺三角形を折り曲げると、左右がぴったり「重なる」ことがわかります。
一度、はさみを使って確かめてみてもいいですね。
「【対称な図形1】二等辺三角形と線対称」プリント一覧
リンクをクリックするとPDFが表示されます。
【対称な図形2】線対称の軸

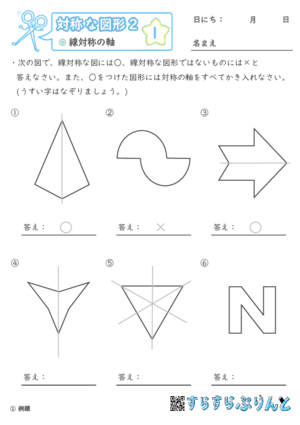
様々な図形に対して、線対称な図形か? 線対称ではない図形か? を判別して「○・×」をつけて、線対称な図形の場合は「対称の軸」を図形に書き入れる問題を集めた学習プリントです。
線対称な図は、どこかで折るとぴったり重なる左右対称な図形です。
対称の軸(ぴったり重なるように折るときの線)が、1本ではなく複数ある図形も存在します。
紙をくるくる回していろいろな角度から図形を見て確かめてみてもいいですね。
よく出る問題は複数回出しています。
これ! という解き方がない分、慣れることで乗り越えられる問題です。
いろんな形があるので楽しみながら解いてみてくださいね。
「【対称な図形2】線対称の軸」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】線対称の軸【対称な図形2】01例題
- 【02】線対称の軸【対称な図形2】02確認
- 【03】線対称の軸【対称な図形2】03確認
- 【04】線対称の軸【対称な図形2】04確認
- 【05】線対称の軸【対称な図形2】05定着
- 【06】線対称の軸【対称な図形2】06定着
- 【07】線対称の軸【対称な図形2】07定着
- 【08】線対称の軸【対称な図形2】08定着
- 【09】線対称の軸【対称な図形2】09定着
- 【10】線対称の軸【対称な図形2】10仕上げ
- 【11】線対称の軸【対称な図形2】11仕上げ
- 【12】線対称の軸【対称な図形2】12仕上げ
- 【13】線対称の軸【対称な図形2】13仕上げ
- 【14】線対称の軸【対称な図形2】14仕上げ
- 【15】線対称の軸【対称な図形2】15力だめし
- 【16】線対称の軸【対称な図形2】16力だめし
【対称な図形3】線対称な図形の対応する点

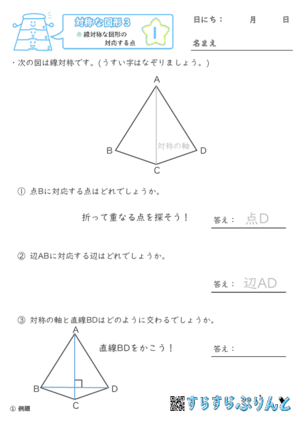
線対称な図形について、対応する辺や点を答える問題を集めた学習プリントです。
線対称な図形が重なるように折るときの線を「対称の軸」ということもこのプリントで学びます。
対称の軸で折って重ねたときに、重なる辺や点のことを「対応する」と言います。
対応する点同士を結んだ線は、対称の軸と垂直に交わります。
『例題』『確認』では、解説もついていてわかりやすいですよ。
『仕上げ』と『力だめし』では、様々な図形に対して、線対称な図形か? 線対称ではない図形か? を判別して「○・×」をつけて、線対称な図形の場合は「対称の軸」を図形に書き入れる問題を混ぜてあります。
「【対称な図形3】線対称な図形の対応する点」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】線対称な図形の対応する点【対称な図形3】01例題
- 【02】線対称な図形の対応する点【対称な図形3】02確認
- 【03】線対称な図形の対応する点【対称な図形3】03確認
- 【04】線対称な図形の対応する点【対称な図形3】04確認
- 【05】線対称な図形の対応する点【対称な図形3】05定着
- 【06】線対称な図形の対応する点【対称な図形3】06定着
- 【07】線対称な図形の対応する点【対称な図形3】07定着
- 【08】線対称な図形の対応する点【対称な図形3】08定着
- 【09】線対称な図形の対応する点【対称な図形3】09定着
- 【10】線対称な図形の対応する点【対称な図形3】10仕上げ
- 【11】線対称な図形の対応する点【対称な図形3】11仕上げ
- 【12】線対称な図形の対応する点【対称な図形3】12仕上げ
- 【13】線対称な図形の対応する点【対称な図形3】13仕上げ
- 【14】線対称な図形の対応する点【対称な図形3】14仕上げ
- 【15】線対称な図形の対応する点【対称な図形3】15力だめし
- 【16】線対称な図形の対応する点【対称な図形3】16力だめし
【対称な図形4】線対称な図形の軸

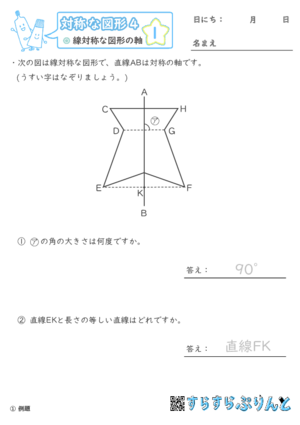
線対称な図形について、対応する点を結ぶ直線と対称の軸との交わり方に関する学習プリントです。
対応する2つの点を結ぶ直線と対称の軸は垂直(90度)に交わります。
また、この交わる点から対応する2つの点までの長さは同じです。
「【対称な図形4】線対称な図形の軸」プリント一覧
リンクをクリックするとPDFが表示されます。
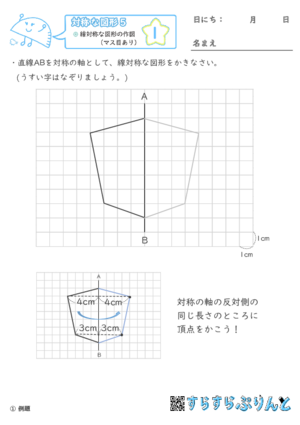
【対称な図形5】線対称な図形の作図(マス目あり)

方眼紙(マス目)の上に線対称な図形の片側だけが書いてあり、残りを作図する問題を集めた学習プリントです。
定規を準備して取り組みましょう。
わかっている頂点から対称の軸に対して垂線を引き、ぴったり同じ長さのところに対応する点をとりましょう。
対称の軸が縦のものと横のもの、両方ありますがどちらも解き方は同じです。
『例題』と『確認』では、書き方の縮小図がついていますので、最初はそれを見ながら真似して解いてみましょう。
『仕上げ』と『力だめし』では、線対称な図形の軸の性質についての問題を混ぜてあります。(【対称な図形4】の類似問題です)
「【対称な図形5】線対称な図形の作図(マス目あり)」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】線対称な図形の作図(マス目あり)【対称な図形5】01例題
- 【02】線対称な図形の作図(マス目あり)【対称な図形5】02確認
- 【03】線対称な図形の作図(マス目あり)【対称な図形5】03確認
- 【04】線対称な図形の作図(マス目あり)【対称な図形5】04確認
- 【05】線対称な図形の作図(マス目あり)【対称な図形5】05定着
- 【06】線対称な図形の作図(マス目あり)【対称な図形5】06定着
- 【07】線対称な図形の作図(マス目あり)【対称な図形5】07定着
- 【08】線対称な図形の作図(マス目あり)【対称な図形5】08定着
- 【09】線対称な図形の作図(マス目あり)【対称な図形5】09定着
- 【10】線対称な図形の作図(マス目あり)【対称な図形5】10仕上げ
- 【11】線対称な図形の作図(マス目あり)【対称な図形5】11仕上げ
- 【12】線対称な図形の作図(マス目あり)【対称な図形5】12仕上げ
- 【13】線対称な図形の作図(マス目あり)【対称な図形5】13仕上げ
- 【14】線対称な図形の作図(マス目あり)【対称な図形5】14仕上げ
- 【15】線対称な図形の作図(マス目あり)【対称な図形5】15力だめし
- 【16】線対称な図形の作図(マス目あり)【対称な図形5】16力だめし
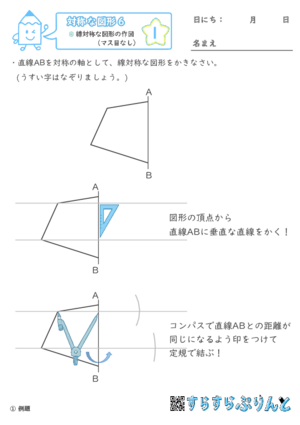
【対称な図形6】線対称な図形の作図(マス目なし)

対称の軸とともに線対称な図形の片側だけが書いてあり、残りを作図する問題を集めた学習プリントです。
方眼紙(マス目)はありません。三角定規とコンパスを準備して取り組みましょう。
まず頂点から対称の軸にむかって垂線を書きます。この垂線は、対称の軸の反対側まで長めに伸ばしましょう。
次に、コンパスで頂点と対称の軸の長さをとります。
対称の軸の反対側に、同じ長さの点をとります。これが頂点になります。
『例題』と『確認』で、作図の手順を図付きで解説しています。
前回のプリントでマス目を数えて同じ長さを見つけていた部分が、コンパスで同じ長さをとるように置き換わるだけなので、考え方は同じですね。
『仕上げ』と『力だめし』では、方眼紙(マス目)の上に線対称な図形の片側だけが書いてあり、残りを作図する問題を混ぜてあります。
「【対称な図形6】線対称な図形の作図(マス目なし)」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】線対称な図形の作図(マス目なし)【対称な図形6】01例題
- 【02】線対称な図形の作図(マス目なし)【対称な図形6】02確認
- 【03】線対称な図形の作図(マス目なし)【対称な図形6】03確認
- 【04】線対称な図形の作図(マス目なし)【対称な図形6】04確認
- 【05】線対称な図形の作図(マス目なし)【対称な図形6】05定着
- 【06】線対称な図形の作図(マス目なし)【対称な図形6】06定着
- 【07】線対称な図形の作図(マス目なし)【対称な図形6】07定着
- 【08】線対称な図形の作図(マス目なし)【対称な図形6】08定着
- 【09】線対称な図形の作図(マス目なし)【対称な図形6】09定着
- 【10】線対称な図形の作図(マス目なし)【対称な図形6】10仕上げ
- 【11】線対称な図形の作図(マス目なし)【対称な図形6】11仕上げ
- 【12】線対称な図形の作図(マス目なし)【対称な図形6】12仕上げ
- 【13】線対称な図形の作図(マス目なし)【対称な図形6】13仕上げ
- 【14】線対称な図形の作図(マス目なし)【対称な図形6】14仕上げ
- 【15】線対称な図形の作図(マス目なし)【対称な図形6】15力だめし
- 【16】線対称な図形の作図(マス目なし)【対称な図形6】16力だめし
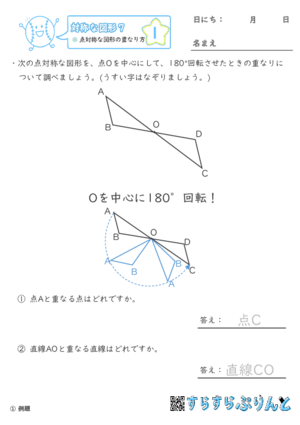
【対称な図形7】点対称な図形の重なり方

点対称な図形が 180°回転したとき、重なる点や辺について答える問題を集めた学習プリントです。
図形を回すということが、突然きかれてもピンとこない生徒さんも多いので、このプリントでは対称の点で図形を回すのを図示しています。
まわった結果、どこの点や辺と重なるのか、具体的にイメージしながら答えることができますよ。
「【対称な図形7】点対称な図形の重なり方」プリント一覧
リンクをクリックするとPDFが表示されます。
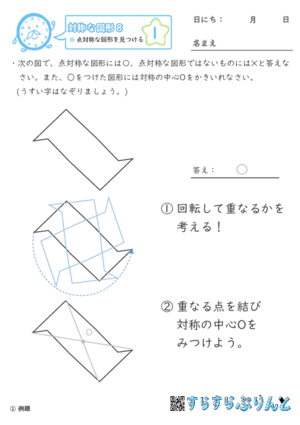
【対称な図形8】点対称な図形を見つける

図形が点対称な図形かどうか判断し、点対称だった場合は「対称の中心O」を書き入れる問題を集めた学習プリントです。
図形の中には、線対称なものや、線対称・点対称のいずれでもないものも混ざっています。
図形を回転させるとどうなるか? イメージしながらこたえましょう。
「対称の中心O」は、対応する点を結んだ直線を複数かくと、その交点として見つけることができますよ。
『仕上げ』と『力だめし』では、点対称な図形が 180°回転したとき重なる点や辺について答える問題を混ぜてあります。
「【対称な図形8】点対称な図形を見つける」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】点対称な図形を見つける【対称な図形8】01例題
- 【02】点対称な図形を見つける【対称な図形8】02確認
- 【03】点対称な図形を見つける【対称な図形8】03確認
- 【04】点対称な図形を見つける【対称な図形8】04確認
- 【05】点対称な図形を見つける【対称な図形8】05定着
- 【06】点対称な図形を見つける【対称な図形8】06定着
- 【07】点対称な図形を見つける【対称な図形8】07定着
- 【08】点対称な図形を見つける【対称な図形8】08定着
- 【09】点対称な図形を見つける【対称な図形8】09定着
- 【10】点対称な図形を見つける【対称な図形8】10仕上げ
- 【11】点対称な図形を見つける【対称な図形8】11仕上げ
- 【12】点対称な図形を見つける【対称な図形8】12仕上げ
- 【13】点対称な図形を見つける【対称な図形8】13仕上げ
- 【14】点対称な図形を見つける【対称な図形8】14仕上げ
- 【15】点対称な図形を見つける【対称な図形8】15力だめし
- 【16】点対称な図形を見つける【対称な図形8】16力だめし