- 【拡大図と縮図1】拡大図と縮図はどれですかプリント数:9
- 【拡大図と縮図2】対応する辺と角プリント数:16
- 【拡大図と縮図3】三角形の拡大図の作図(コンパス)プリント数:16
- 【拡大図と縮図4】三角形の縮図の作図(コンパス)プリント数:16
- 【拡大図と縮図5】ある頂点を中心とした拡大図の作図プリント数:16
- 【拡大図と縮図6】ある頂点を中心とした縮図の作図プリント数:16
- 【拡大図と縮図7】地図(縮図)と実際の距離プリント数:9
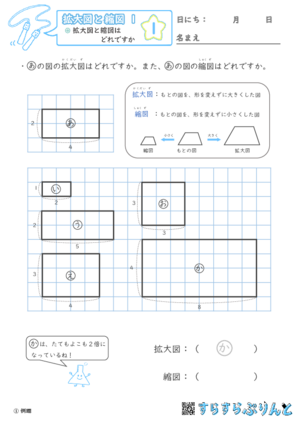
【拡大図と縮図1】拡大図と縮図はどれですか

拡大図と縮図を選ぶ問題です。
辺の比で求めるのが正しいやり方になりますが、まずは拡大と縮小の言葉の意味が分かれば大丈夫です!
すらすらと選べるようになったら次のプリントに進みましょう。
「【拡大図と縮図1】拡大図と縮図はどれですか」プリント一覧
リンクをクリックするとPDFが表示されます。
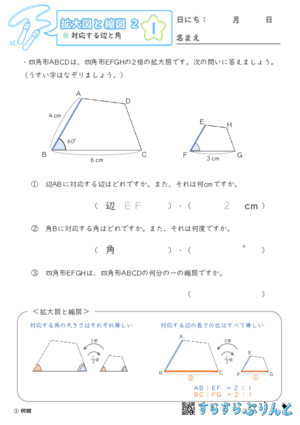
【拡大図と縮図2】対応する辺と角

対応する辺や角の問題です。
同じ形に見えるのは辺の比や角が等しいからということが分かりますね。
アルファベットが多く間違えやすい問題です。図に○をつけたり、角度を書きこんだりしてミスを防ぎましょう。
「【拡大図と縮図2】対応する辺と角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】対応する辺と角【拡大図と縮図2】01例題
- 【02】対応する辺と角【拡大図と縮図2】02確認
- 【03】対応する辺と角【拡大図と縮図2】03確認
- 【04】対応する辺と角【拡大図と縮図2】04確認
- 【05】対応する辺と角【拡大図と縮図2】05定着
- 【06】対応する辺と角【拡大図と縮図2】06定着
- 【07】対応する辺と角【拡大図と縮図2】07定着
- 【08】対応する辺と角【拡大図と縮図2】08定着
- 【09】対応する辺と角【拡大図と縮図2】09定着
- 【10】対応する辺と角【拡大図と縮図2】10仕上げ
- 【11】対応する辺と角【拡大図と縮図2】11仕上げ
- 【12】対応する辺と角【拡大図と縮図2】12仕上げ
- 【13】対応する辺と角【拡大図と縮図2】13仕上げ
- 【14】対応する辺と角【拡大図と縮図2】14仕上げ
- 【15】対応する辺と角【拡大図と縮図2】15力だめし
- 【16】対応する辺と角【拡大図と縮図2】16力だめし
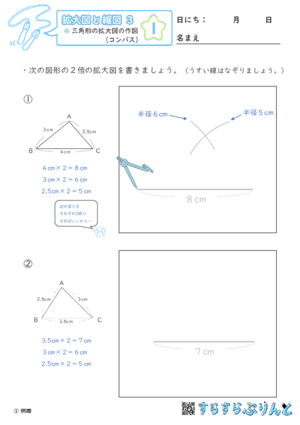
【拡大図と縮図3】三角形の拡大図の作図(コンパス)

拡大図を作図する学習プリントです。全ての辺の長さを2倍にして2倍の拡大図を描きます。
作図の手順は合同な図形の作図と似ていて、定規とコンパスを使います。
1mmくらいはズレでも良いです。拡大図を描く手順を身につけましょう。
「【拡大図と縮図3】三角形の拡大図の作図(コンパス)」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】三角形の拡大図の作図(コンパス)【拡大図と縮図3】01例題
- 【02】三角形の拡大図の作図(コンパス)【拡大図と縮図3】02確認
- 【03】三角形の拡大図の作図(コンパス)【拡大図と縮図3】03確認
- 【04】三角形の拡大図の作図(コンパス)【拡大図と縮図3】04確認
- 【05】三角形の拡大図の作図(コンパス)【拡大図と縮図3】05定着
- 【06】三角形の拡大図の作図(コンパス)【拡大図と縮図3】06定着
- 【07】三角形の拡大図の作図(コンパス)【拡大図と縮図3】07定着
- 【08】三角形の拡大図の作図(コンパス)【拡大図と縮図3】08定着
- 【09】三角形の拡大図の作図(コンパス)【拡大図と縮図3】09定着
- 【10】三角形の拡大図の作図(コンパス)【拡大図と縮図3】10仕上げ
- 【11】三角形の拡大図の作図(コンパス)【拡大図と縮図3】11仕上げ
- 【12】三角形の拡大図の作図(コンパス)【拡大図と縮図3】12仕上げ
- 【13】三角形の拡大図の作図(コンパス)【拡大図と縮図3】13仕上げ
- 【14】三角形の拡大図の作図(コンパス)【拡大図と縮図3】14仕上げ
- 【15】三角形の拡大図の作図(コンパス)【拡大図と縮図3】15力だめし
- 【16】三角形の拡大図の作図(コンパス)【拡大図と縮図3】16力だめし
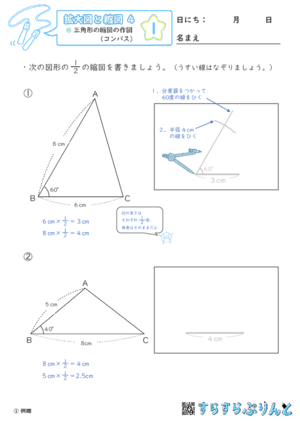
【拡大図と縮図4】三角形の縮図の作図(コンパス)

二分の一の縮図を作図する学習プリントです。すべての辺の長さを二分の一にして描きます。
図が描けたら、もとの図形と同じ形(相似)になっているか確認しましょう。
「【拡大図と縮図4】三角形の縮図の作図(コンパス)」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】三角形の縮図の作図(コンパス)【拡大図と縮図4】01例題
- 【02】三角形の縮図の作図(コンパス)【拡大図と縮図4】02確認
- 【03】三角形の縮図の作図(コンパス)【拡大図と縮図4】03確認
- 【04】三角形の縮図の作図(コンパス)【拡大図と縮図4】04確認
- 【05】三角形の縮図の作図(コンパス)【拡大図と縮図4】05定着
- 【06】三角形の縮図の作図(コンパス)【拡大図と縮図4】06定着
- 【07】三角形の縮図の作図(コンパス)【拡大図と縮図4】07定着
- 【08】三角形の縮図の作図(コンパス)【拡大図と縮図4】08定着
- 【09】三角形の縮図の作図(コンパス)【拡大図と縮図4】09定着
- 【10】三角形の縮図の作図(コンパス)【拡大図と縮図4】10仕上げ
- 【11】三角形の縮図の作図(コンパス)【拡大図と縮図4】11仕上げ
- 【12】三角形の縮図の作図(コンパス)【拡大図と縮図4】12仕上げ
- 【13】三角形の縮図の作図(コンパス)【拡大図と縮図4】13仕上げ
- 【14】三角形の縮図の作図(コンパス)【拡大図と縮図4】14仕上げ
- 【15】三角形の縮図の作図(コンパス)【拡大図と縮図4】15力だめし
- 【16】三角形の縮図の作図(コンパス)【拡大図と縮図4】16力だめし
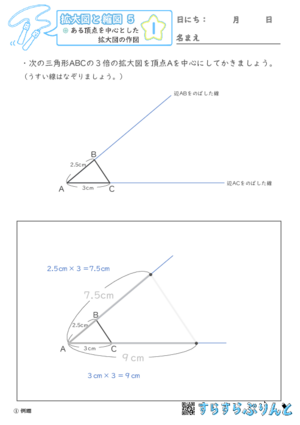
【拡大図と縮図5】ある頂点を中心とした拡大図の作図

このプリントでは1つの頂点を中心として2倍,3倍の拡大図を描きます。
基準となる直線上で辺を延長するイメージになります。
まず辺の長さを計算して書いておくと間違えにくいです。
できた図形がもとの図形と同じ形になっていることも合わせて確認しましょう。
「【拡大図と縮図5】ある頂点を中心とした拡大図の作図」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】ある頂点を中心とした拡大図の作図【拡大図と縮図5】01例題
- 【02】ある頂点を中心とした拡大図の作図【拡大図と縮図5】02確認
- 【03】ある頂点を中心とした拡大図の作図【拡大図と縮図5】03確認
- 【04】ある頂点を中心とした拡大図の作図【拡大図と縮図5】04確認
- 【05】ある頂点を中心とした拡大図の作図【拡大図と縮図5】05定着
- 【06】ある頂点を中心とした拡大図の作図【拡大図と縮図5】06定着
- 【07】ある頂点を中心とした拡大図の作図【拡大図と縮図5】07定着
- 【08】ある頂点を中心とした拡大図の作図【拡大図と縮図5】08定着
- 【09】ある頂点を中心とした拡大図の作図【拡大図と縮図5】09定着
- 【10】ある頂点を中心とした拡大図の作図【拡大図と縮図5】10仕上げ
- 【11】ある頂点を中心とした拡大図の作図【拡大図と縮図5】11仕上げ
- 【12】ある頂点を中心とした拡大図の作図【拡大図と縮図5】12仕上げ
- 【13】ある頂点を中心とした拡大図の作図【拡大図と縮図5】13仕上げ
- 【14】ある頂点を中心とした拡大図の作図【拡大図と縮図5】14仕上げ
- 【15】ある頂点を中心とした拡大図の作図【拡大図と縮図5】15力だめし
- 【16】ある頂点を中心とした拡大図の作図【拡大図と縮図5】16力だめし
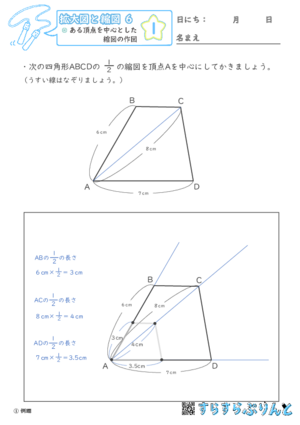
【拡大図と縮図6】ある頂点を中心とした縮図の作図

2分の1の縮図を描く学習プリントです。
印刷するときは印刷設定の「実際のサイズ」にチェックを入れて印刷してください。
印刷した大きさが多少異なっていても、計算した値で作図ができていればOKです!
「【拡大図と縮図6】ある頂点を中心とした縮図の作図」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】ある頂点を中心とした縮図の作図【拡大図と縮図6】01例題
- 【02】ある頂点を中心とした縮図の作図【拡大図と縮図6】02確認
- 【03】ある頂点を中心とした縮図の作図【拡大図と縮図6】03確認
- 【04】ある頂点を中心とした縮図の作図【拡大図と縮図6】04確認
- 【05】ある頂点を中心とした縮図の作図【拡大図と縮図6】05定着
- 【06】ある頂点を中心とした縮図の作図【拡大図と縮図6】06定着
- 【07】ある頂点を中心とした縮図の作図【拡大図と縮図6】07定着
- 【08】ある頂点を中心とした縮図の作図【拡大図と縮図6】08定着
- 【09】ある頂点を中心とした縮図の作図【拡大図と縮図6】09定着
- 【10】ある頂点を中心とした縮図の作図【拡大図と縮図6】10仕上げ
- 【11】ある頂点を中心とした縮図の作図【拡大図と縮図6】11仕上げ
- 【12】ある頂点を中心とした縮図の作図【拡大図と縮図6】12仕上げ
- 【13】ある頂点を中心とした縮図の作図【拡大図と縮図6】13仕上げ
- 【14】ある頂点を中心とした縮図の作図【拡大図と縮図6】14仕上げ
- 【15】ある頂点を中心とした縮図の作図【拡大図と縮図6】15力だめし
- 【16】ある頂点を中心とした縮図の作図【拡大図と縮図6】16力だめし
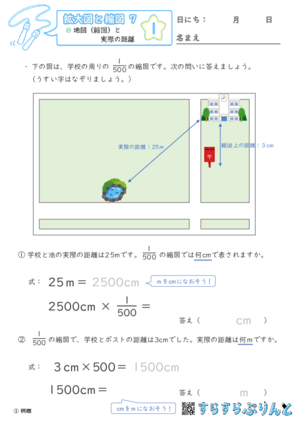
【拡大図と縮図7】地図(縮図)と実際の距離

縮図の利用の学習プリントです。
これを応用して行うのが測量ですね。建設や地図を作るために必要不可欠な技術です。
身近な場所の地図をみて、だいたい何mか計算してみましょう! 理解が深まります。
「【拡大図と縮図7】地図(縮図)と実際の距離」プリント一覧
リンクをクリックするとPDFが表示されます。