- 【単位量あたりの大きさ1】こみぐあいを調べるプリント数:16
- 【単位量あたりの大きさ2】こみぐあいを比べるプリント数:16
- 【単位量あたりの大きさ3】1あたりの量を求めるプリント数:16
- 【単位量あたりの大きさ4】単位量から比べられる量を求めるプリント数:16
- 【単位量あたりの大きさ5】単位量を求めて比べるプリント数:16
- 【単位量あたりの大きさ6】人口密度を求めるプリント数:16
- 【単位量あたりの大きさ7】同じ距離の速さを比べるプリント数:2
- 【単位量あたりの大きさ8】1分あたりに歩いた道のりプリント数:16
- 【単位量あたりの大きさ9】1秒あたりに走った道のりプリント数:16
- 【単位量あたりの大きさ10】1mあたりにかかる時間プリント数:16
- 【単位量あたりの大きさ11】速さを求めるプリント数:16
- 【単位量あたりの大きさ12】時速と分速を変かんするプリント数:16
- 【単位量あたりの大きさ13】分速と秒速を変かんするプリント数:16
- 【単位量あたりの大きさ14】時速と秒速を変かんするプリント数:16
- 【単位量あたりの大きさ15】道のりを求めるプリント数:16
- 【単位量あたりの大きさ16】道のりを求めて単位を変えるプリント数:16
- 【単位量あたりの大きさ17】時間の単位を変えて道のりを求めるプリント数:16
- 【単位量あたりの大きさ18】時間を求めるプリント数:16
- 【単位量あたりの大きさ19】道のりの単位を変えて時間を求めるプリント数:16
- 【単位量あたりの大きさ20】時間を求めて単位を直すプリント数:16
- 【単位量あたりの大きさ21】仕事の速さを比べるプリント数:16
- 【単位量あたりの大きさ22】仕事の速さから仕事量を求めるプリント数:16
【単位量あたりの大きさ1】こみぐあいを調べる

こみぐあいについて、考える問題を集めた学習プリントです。
①同じ広さにいる、人数が違うとき
②同じ人数だけど、広さが違うとき
の両方について考えます。
個数あたりの値段の問題や、広さあたりの花の本数や動物の数の問題もあります。
単位あたりの数を計算することで、こみぐあいがわかりますね!
「【単位量あたりの大きさ1】こみぐあいを調べる」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】こみぐあいを調べる【単位量あたりの大きさ1】01例題
- 【02】こみぐあいを調べる【単位量あたりの大きさ1】02確認
- 【03】こみぐあいを調べる【単位量あたりの大きさ1】03確認
- 【04】こみぐあいを調べる【単位量あたりの大きさ1】04確認
- 【05】こみぐあいを調べる【単位量あたりの大きさ1】05定着
- 【06】こみぐあいを調べる【単位量あたりの大きさ1】06定着
- 【07】こみぐあいを調べる【単位量あたりの大きさ1】07定着
- 【08】こみぐあいを調べる【単位量あたりの大きさ1】08定着
- 【09】こみぐあいを調べる【単位量あたりの大きさ1】09定着
- 【10】こみぐあいを調べる【単位量あたりの大きさ1】10仕上げ
- 【11】こみぐあいを調べる【単位量あたりの大きさ1】11仕上げ
- 【12】こみぐあいを調べる【単位量あたりの大きさ1】12仕上げ
- 【13】こみぐあいを調べる【単位量あたりの大きさ1】13仕上げ
- 【14】こみぐあいを調べる【単位量あたりの大きさ1】14仕上げ
- 【15】こみぐあいを調べる【単位量あたりの大きさ1】15力だめし
- 【16】こみぐあいを調べる【単位量あたりの大きさ1】16力だめし
【単位量あたりの大きさ2】こみぐあいを比べる

表をみて3つのこみぐあいを比べる問題です。
こんでいる順や、1個あたりのねだんが高い順に並べかえられるようになりましょう。
①広さや数(単位)が同じ
②人数や値段(量)が同じ
③どちらも違う
の3パターンを聞かれます。
③のときは、単位あたりの数量を比べる式を2つ作りましょう。
「【単位量あたりの大きさ2】こみぐあいを比べる」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】こみぐあいを比べる【単位量あたりの大きさ2】01例題
- 【02】こみぐあいを比べる【単位量あたりの大きさ2】02確認
- 【03】こみぐあいを比べる【単位量あたりの大きさ2】03確認
- 【04】こみぐあいを比べる【単位量あたりの大きさ2】04確認
- 【05】こみぐあいを比べる【単位量あたりの大きさ2】05定着
- 【06】こみぐあいを比べる【単位量あたりの大きさ2】06定着
- 【07】こみぐあいを比べる【単位量あたりの大きさ2】07定着
- 【08】こみぐあいを比べる【単位量あたりの大きさ2】08定着
- 【09】こみぐあいを比べる【単位量あたりの大きさ2】09定着
- 【10】こみぐあいを比べる【単位量あたりの大きさ2】10仕上げ
- 【11】こみぐあいを比べる【単位量あたりの大きさ2】11仕上げ
- 【12】こみぐあいを比べる【単位量あたりの大きさ2】12仕上げ
- 【13】こみぐあいを比べる【単位量あたりの大きさ2】13仕上げ
- 【14】こみぐあいを比べる【単位量あたりの大きさ2】14仕上げ
- 【15】こみぐあいを比べる【単位量あたりの大きさ2】15力だめし
- 【16】こみぐあいを比べる【単位量あたりの大きさ2】16力だめし
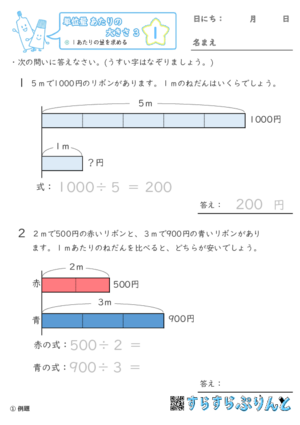
【単位量あたりの大きさ3】1あたりの量を求める

1あたりの量を求める問題を集めた学習プリントです。
長さもねだんも異なるリボンでも、1mあたりのねだんを求めることで、どちらが安いか比べられますね。
『例題』と『確認』ではリボン図を、『定着』以降では比例数直線を使ってヒントを出しています。
図の読み取りにも慣れると、これからの学習でも役立ちますよ!
「【単位量あたりの大きさ3】1あたりの量を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】1あたりの量を求める【単位量あたりの大きさ3】01例題
- 【02】1あたりの量を求める【単位量あたりの大きさ3】02確認
- 【03】1あたりの量を求める【単位量あたりの大きさ3】03確認
- 【04】1あたりの量を求める【単位量あたりの大きさ3】04確認
- 【05】1あたりの量を求める【単位量あたりの大きさ3】05定着
- 【06】1あたりの量を求める【単位量あたりの大きさ3】06定着
- 【07】1あたりの量を求める【単位量あたりの大きさ3】07定着
- 【08】1あたりの量を求める【単位量あたりの大きさ3】08定着
- 【09】1あたりの量を求める【単位量あたりの大きさ3】09定着
- 【10】1あたりの量を求める【単位量あたりの大きさ3】10仕上げ
- 【11】1あたりの量を求める【単位量あたりの大きさ3】11仕上げ
- 【12】1あたりの量を求める【単位量あたりの大きさ3】12仕上げ
- 【13】1あたりの量を求める【単位量あたりの大きさ3】13仕上げ
- 【14】1あたりの量を求める【単位量あたりの大きさ3】14仕上げ
- 【15】1あたりの量を求める【単位量あたりの大きさ3】15力だめし
- 【16】1あたりの量を求める【単位量あたりの大きさ3】16力だめし
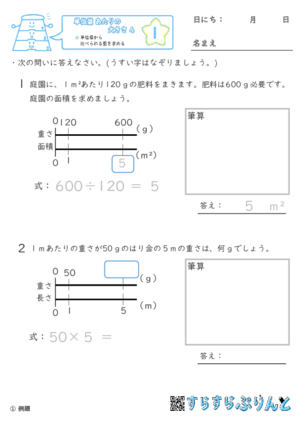
【単位量あたりの大きさ4】単位量から比べられる量を求める

1単位あたりの量がわかっていて、条件をみたす量や単位量を求める問題です。
例えば「1㎡あたり使う肥料の量がわかっていて、指定の重さの肥料が必要な時、広さはどれくらいか?」という問題や、「広さが5㎡の時に使う肥料の量は?」という問題になります。
『定着』からは、量をあらわす単位として「gとkg」「dLとL」が出てきて、単位をあわせて計算する問題も出てきます。
『仕上げ』と『力だめし』には、1あたりの量を求める問題も混ぜてあります。
「【単位量あたりの大きさ4】単位量から比べられる量を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】単位量から比べられる量を求める【単位量あたりの大きさ4】01例題
- 【02】単位量から比べられる量を求める【単位量あたりの大きさ4】02確認
- 【03】単位量から比べられる量を求める【単位量あたりの大きさ4】03確認
- 【04】単位量から比べられる量を求める【単位量あたりの大きさ4】04確認
- 【05】単位量から比べられる量を求める【単位量あたりの大きさ4】05定着
- 【06】単位量から比べられる量を求める【単位量あたりの大きさ4】06定着
- 【07】単位量から比べられる量を求める【単位量あたりの大きさ4】07定着
- 【08】単位量から比べられる量を求める【単位量あたりの大きさ4】08定着
- 【09】単位量から比べられる量を求める【単位量あたりの大きさ4】09定着
- 【10】単位量から比べられる量を求める【単位量あたりの大きさ4】10仕上げ
- 【11】単位量から比べられる量を求める【単位量あたりの大きさ4】11仕上げ
- 【12】単位量から比べられる量を求める【単位量あたりの大きさ4】12仕上げ
- 【13】単位量から比べられる量を求める【単位量あたりの大きさ4】13仕上げ
- 【14】単位量から比べられる量を求める【単位量あたりの大きさ4】14仕上げ
- 【15】単位量から比べられる量を求める【単位量あたりの大きさ4】15力だめし
- 【16】単位量から比べられる量を求める【単位量あたりの大きさ4】16力だめし
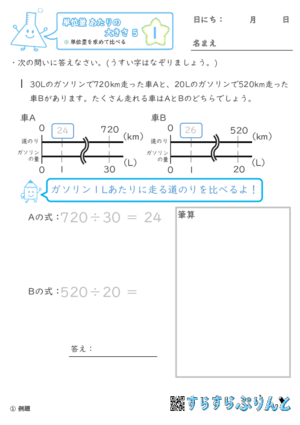
【単位量あたりの大きさ5】単位量を求めて比べる

単位量を求めてから比較したり、求めた単位量から問われている数量を求める問題を集めた学習プリントです。
・2つの車のガソリン1Lあたりに走ることのできる距離をそれぞれ求めて比較する問題
・定められた距離を走るために必要なガソリンの量を求める問題
の2種類の問題を入れています。
『仕上げ』と『力だめし』では、【単位量あたりの大きさ4】単位量から比べられる量を求めるの問題を混ぜてあります。
「【単位量あたりの大きさ5】単位量を求めて比べる」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】単位量を求めて比べる【単位量あたりの大きさ5】01例題
- 【02】単位量を求めて比べる【単位量あたりの大きさ5】02確認
- 【03】単位量を求めて比べる【単位量あたりの大きさ5】03確認
- 【04】単位量を求めて比べる【単位量あたりの大きさ5】04確認
- 【05】単位量を求めて比べる【単位量あたりの大きさ5】05定着
- 【06】単位量を求めて比べる【単位量あたりの大きさ5】06定着
- 【07】単位量を求めて比べる【単位量あたりの大きさ5】07定着
- 【08】単位量を求めて比べる【単位量あたりの大きさ5】08定着
- 【09】単位量を求めて比べる【単位量あたりの大きさ5】09定着
- 【10】単位量を求めて比べる【単位量あたりの大きさ5】10仕上げ
- 【11】単位量を求めて比べる【単位量あたりの大きさ5】11仕上げ
- 【12】単位量を求めて比べる【単位量あたりの大きさ5】12仕上げ
- 【13】単位量を求めて比べる【単位量あたりの大きさ5】13仕上げ
- 【14】単位量を求めて比べる【単位量あたりの大きさ5】14仕上げ
- 【15】単位量を求めて比べる【単位量あたりの大きさ5】15力だめし
- 【16】単位量を求めて比べる【単位量あたりの大きさ5】16力だめし
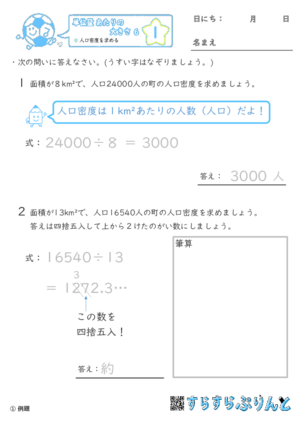
【単位量あたりの大きさ6】人口密度を求める

人口密度を求める問題を集めた学習プリントです。
人口密度は1km²あたりの人口です。
「人口÷面積」で求めましょう。
・答えを四捨五入をする問題
・表を参考に、ぞれぞれの人口密度を求める問題
も、入れてあります。
人口密度の問題は扱う数字も大きく計算間違いもおきやすいです。
また、人口の単位が(人)の問題と(万人)の問題がどちらもあります。
『仕上げ』と『力だめし』では、【単位量あたりの大きさ5】単位量を求めて比べるの問題も混ぜてあります。
「【単位量あたりの大きさ6】人口密度を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】人口密度を求める【単位量あたりの大きさ6】01例題
- 【02】人口密度を求める【単位量あたりの大きさ6】02確認
- 【03】人口密度を求める【単位量あたりの大きさ6】03確認
- 【04】人口密度を求める【単位量あたりの大きさ6】04確認
- 【05】人口密度を求める【単位量あたりの大きさ6】05定着
- 【06】人口密度を求める【単位量あたりの大きさ6】06定着
- 【07】人口密度を求める【単位量あたりの大きさ6】07定着
- 【08】人口密度を求める【単位量あたりの大きさ6】08定着
- 【09】人口密度を求める【単位量あたりの大きさ6】09定着
- 【10】人口密度を求める【単位量あたりの大きさ6】10仕上げ
- 【11】人口密度を求める【単位量あたりの大きさ6】11仕上げ
- 【12】人口密度を求める【単位量あたりの大きさ6】12仕上げ
- 【13】人口密度を求める【単位量あたりの大きさ6】13仕上げ
- 【14】人口密度を求める【単位量あたりの大きさ6】14仕上げ
- 【15】人口密度を求める【単位量あたりの大きさ6】15力だめし
- 【16】人口密度を求める【単位量あたりの大きさ6】16力だめし
【単位量あたりの大きさ7】同じ距離の速さを比べる

速さの導入のプリントです。
同じ距離を3人の中で、一番速い人を答える問題です。
表をみて、速くゴールについた人を選びましょう。
「【単位量あたりの大きさ7】同じ距離の速さを比べる」プリント一覧
リンクをクリックするとPDFが表示されます。
【単位量あたりの大きさ8】1分あたりに歩いた道のり

3人の帰宅にかかった時間と道のりを記録した表をもとに、歩く速さを比べる問題です。
道のりが同じときや、かかった時間が同じとき、どちらが速いかすぐ答えられるようになりましょう。
3人を歩くのが速い順に並べる問題は、それぞれが1分あたりに歩いた道のりを計算すると解けますね!
「【単位量あたりの大きさ8】1分あたりに歩いた道のり」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】1分あたりに歩いた道のり【単位量あたりの大きさ8】01例題
- 【02】1分あたりに歩いた道のり【単位量あたりの大きさ8】02確認
- 【03】1分あたりに歩いた道のり【単位量あたりの大きさ8】03確認
- 【04】1分あたりに歩いた道のり【単位量あたりの大きさ8】04確認
- 【05】1分あたりに歩いた道のり【単位量あたりの大きさ8】05定着
- 【06】1分あたりに歩いた道のり【単位量あたりの大きさ8】06定着
- 【07】1分あたりに歩いた道のり【単位量あたりの大きさ8】07定着
- 【08】1分あたりに歩いた道のり【単位量あたりの大きさ8】08定着
- 【09】1分あたりに歩いた道のり【単位量あたりの大きさ8】09定着
- 【10】1分あたりに歩いた道のり【単位量あたりの大きさ8】10仕上げ
- 【11】1分あたりに歩いた道のり【単位量あたりの大きさ8】11仕上げ
- 【12】1分あたりに歩いた道のり【単位量あたりの大きさ8】12仕上げ
- 【13】1分あたりに歩いた道のり【単位量あたりの大きさ8】13仕上げ
- 【14】1分あたりに歩いた道のり【単位量あたりの大きさ8】14仕上げ
- 【15】1分あたりに歩いた道のり【単位量あたりの大きさ8】15力だめし
- 【16】1分あたりに歩いた道のり【単位量あたりの大きさ8】16力だめし
【単位量あたりの大きさ9】1秒あたりに走った道のり

「1単位あたりの量」 をもとに、全体の量や単位あたりの量を求める学習プリントです。
ここでは数量の関係を理解するために、比例数直線(数直線を使った関係の図示) を活用します。
★学べるポイント
1㎡あたりの肥料の量 から 必要な面積 を求める。
1mあたりの価格 から 合計の値段 を求める。
単位(g, kg / dL, Lなど)をそろえて計算する。
比例数直線を使って、数量の関係を視覚的に整理する。
このプリントを活用して、「単位あたりの量」と「比例数直線」を使った計算力をしっかり身につけましょう!
「【単位量あたりの大きさ9】1秒あたりに走った道のり」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】1秒あたりに走った道のり【単位量あたりの大きさ9】01例題
- 【02】1秒あたりに走った道のり【単位量あたりの大きさ9】02確認
- 【03】1秒あたりに走った道のり【単位量あたりの大きさ9】03確認
- 【04】1秒あたりに走った道のり【単位量あたりの大きさ9】04確認
- 【05】1秒あたりに走った道のり【単位量あたりの大きさ9】05定着
- 【06】1秒あたりに走った道のり【単位量あたりの大きさ9】06定着
- 【07】1秒あたりに走った道のり【単位量あたりの大きさ9】07定着
- 【08】1秒あたりに走った道のり【単位量あたりの大きさ9】08定着
- 【09】1秒あたりに走った道のり【単位量あたりの大きさ9】09定着
- 【10】1秒あたりに走った道のり【単位量あたりの大きさ9】10仕上げ
- 【11】1秒あたりに走った道のり【単位量あたりの大きさ9】11仕上げ
- 【12】1秒あたりに走った道のり【単位量あたりの大きさ9】12仕上げ
- 【13】1秒あたりに走った道のり【単位量あたりの大きさ9】13仕上げ
- 【14】1秒あたりに走った道のり【単位量あたりの大きさ9】14仕上げ
- 【15】1秒あたりに走った道のり【単位量あたりの大きさ9】15力だめし
- 【16】1秒あたりに走った道のり【単位量あたりの大きさ9】16力だめし
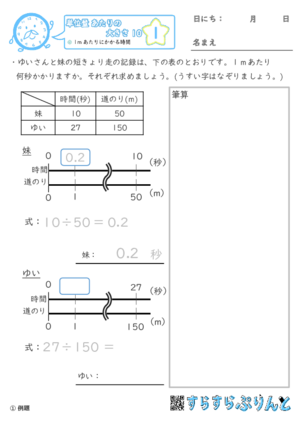
【単位量あたりの大きさ10】1mあたりにかかる時間

表をもとに、1mあたりにかかった秒数を求める問題のプリントです。
2人のきょうだいが時間と道のりが異なる短きょり走をした記録から、
「時間÷道のり」で、1mあたりにかかった秒数を計算しましょう。
『仕上げ』と『力だめし』では、1秒あたりに進んだ(走った)道のりを求める問題を混ぜてあります。
「【単位量あたりの大きさ10】1mあたりにかかる時間」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】1mあたりにかかる時間【単位量あたりの大きさ10】01例題
- 【02】1mあたりにかかる時間【単位量あたりの大きさ10】02確認
- 【03】1mあたりにかかる時間【単位量あたりの大きさ10】03確認
- 【04】1mあたりにかかる時間【単位量あたりの大きさ10】04確認
- 【05】1mあたりにかかる時間【単位量あたりの大きさ10】05定着
- 【06】1mあたりにかかる時間【単位量あたりの大きさ10】06定着
- 【07】1mあたりにかかる時間【単位量あたりの大きさ10】07定着
- 【08】1mあたりにかかる時間【単位量あたりの大きさ10】08定着
- 【09】1mあたりにかかる時間【単位量あたりの大きさ10】09定着
- 【10】1mあたりにかかる時間【単位量あたりの大きさ10】10仕上げ
- 【11】1mあたりにかかる時間【単位量あたりの大きさ10】11仕上げ
- 【12】1mあたりにかかる時間【単位量あたりの大きさ10】12仕上げ
- 【13】1mあたりにかかる時間【単位量あたりの大きさ10】13仕上げ
- 【14】1mあたりにかかる時間【単位量あたりの大きさ10】14仕上げ
- 【15】1mあたりにかかる時間【単位量あたりの大きさ10】15力だめし
- 【16】1mあたりにかかる時間【単位量あたりの大きさ10】16力だめし
【単位量あたりの大きさ11】速さを求める

速さを求める問題を集めた学習プリントです。
『例題』と『確認』では、「時速」「分速」「秒速」の言葉の解説をしています。
時間あたりの道のりを求めるために、「道のり÷時間」をする問題はこれまでもやってきましたが、
速さとして聞かれたときは、「時速〇km」「分速〇m」……と、答えの書き方がかわります。
問題文をよく読んで、単位も正しく書きましょう。
「【単位量あたりの大きさ11】速さを求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】速さを求める【単位量あたりの大きさ11】01例題
- 【02】速さを求める【単位量あたりの大きさ11】02確認
- 【03】速さを求める【単位量あたりの大きさ11】03確認
- 【04】速さを求める【単位量あたりの大きさ11】04確認
- 【05】速さを求める【単位量あたりの大きさ11】05定着
- 【06】速さを求める【単位量あたりの大きさ11】06定着
- 【07】速さを求める【単位量あたりの大きさ11】07定着
- 【08】速さを求める【単位量あたりの大きさ11】08定着
- 【09】速さを求める【単位量あたりの大きさ11】09定着
- 【10】速さを求める【単位量あたりの大きさ11】10仕上げ
- 【11】速さを求める【単位量あたりの大きさ11】11仕上げ
- 【12】速さを求める【単位量あたりの大きさ11】12仕上げ
- 【13】速さを求める【単位量あたりの大きさ11】13仕上げ
- 【14】速さを求める【単位量あたりの大きさ11】14仕上げ
- 【15】速さを求める【単位量あたりの大きさ11】15力だめし
- 【16】速さを求める【単位量あたりの大きさ11】16力だめし
【単位量あたりの大きさ12】時速と分速を変かんする

時速・分速の変換をする問題を集めた学習プリントです。
・時速を分速に変換する問題
・分速を時速に変換する問題
・それぞれ「m」と「km」の単位も変換する問題
を、練習できます。
・時速を分速になおすときは÷60
・分速を時速になおすときは×60
『例題』と『確認』では変換のコツを大きく書いてあります。
「【単位量あたりの大きさ12】時速と分速を変かんする」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】時速と分速を変かんする【単位量あたりの大きさ12】01例題
- 【02】時速と分速を変かんする【単位量あたりの大きさ12】02確認
- 【03】時速と分速を変かんする【単位量あたりの大きさ12】03確認
- 【04】時速と分速を変かんする【単位量あたりの大きさ12】04確認
- 【05】時速と分速を変かんする【単位量あたりの大きさ12】05定着
- 【06】時速と分速を変かんする【単位量あたりの大きさ12】06定着
- 【07】時速と分速を変かんする【単位量あたりの大きさ12】07定着
- 【08】時速と分速を変かんする【単位量あたりの大きさ12】08定着
- 【09】時速と分速を変かんする【単位量あたりの大きさ12】09定着
- 【10】時速と分速を変かんする【単位量あたりの大きさ12】10仕上げ
- 【11】時速と分速を変かんする【単位量あたりの大きさ12】11仕上げ
- 【12】時速と分速を変かんする【単位量あたりの大きさ12】12仕上げ
- 【13】時速と分速を変かんする【単位量あたりの大きさ12】13仕上げ
- 【14】時速と分速を変かんする【単位量あたりの大きさ12】14仕上げ
- 【15】時速と分速を変かんする【単位量あたりの大きさ12】15力だめし
- 【16】時速と分速を変かんする【単位量あたりの大きさ12】16力だめし
【単位量あたりの大きさ13】分速と秒速を変かんする

分速・秒速の変換をする問題を集めた学習プリントです。
・分速を秒速に変換する問題
・秒速を分速に変換する問題
・それぞれ「cm」と「m」の単位も変換する問題
を、練習できます。
・分速を秒速になおすときは÷60
・秒速を分速になおすときは×60
たくさん練習してマスターしましょう。
『仕上げ』と『力だめし』では分速・時速の変換をする問題がたまに混ざっています。
「【単位量あたりの大きさ13】分速と秒速を変かんする」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】分速と秒速を変かんする【単位量あたりの大きさ13】01例題
- 【02】分速と秒速を変かんする【単位量あたりの大きさ13】02確認
- 【03】分速と秒速を変かんする【単位量あたりの大きさ13】03確認
- 【04】分速と秒速を変かんする【単位量あたりの大きさ13】04確認
- 【05】分速と秒速を変かんする【単位量あたりの大きさ13】05定着
- 【06】分速と秒速を変かんする【単位量あたりの大きさ13】06定着
- 【07】分速と秒速を変かんする【単位量あたりの大きさ13】07定着
- 【08】分速と秒速を変かんする【単位量あたりの大きさ13】08定着
- 【09】分速と秒速を変かんする【単位量あたりの大きさ13】09定着
- 【10】分速と秒速を変かんする【単位量あたりの大きさ13】10仕上げ
- 【11】分速と秒速を変かんする【単位量あたりの大きさ13】11仕上げ
- 【12】分速と秒速を変かんする【単位量あたりの大きさ13】12仕上げ
- 【13】分速と秒速を変かんする【単位量あたりの大きさ13】13仕上げ
- 【14】分速と秒速を変かんする【単位量あたりの大きさ13】14仕上げ
- 【15】分速と秒速を変かんする【単位量あたりの大きさ13】15力だめし
- 【16】分速と秒速を変かんする【単位量あたりの大きさ13】16力だめし
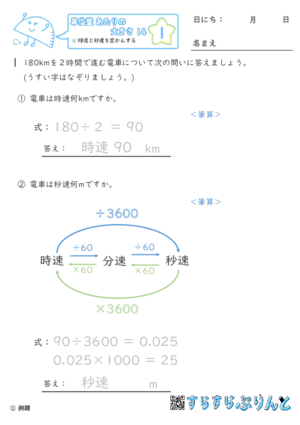
【単位量あたりの大きさ14】時速と秒速を変かんする

時速・秒速の変換をする問題を集めた学習プリントです。
・時速を秒速に変換する問題
・秒速を時速に変換する問題
・それぞれ「m」と「km」の単位も変換する問題
を、練習できます。
・時速を秒速になおすときは÷3600
・秒速を時速になおすときは×3600
数字が大きくなってきました。
計算スペースで途中式を残して見直しをできるようにしましょう。
『仕上げ』と『力だめし』では時速・分速・秒速を変換をする問題が全て入っています。
「【単位量あたりの大きさ14】時速と秒速を変かんする」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】時速と秒速を変かんする【単位量あたりの大きさ14】01例題
- 【02】時速と秒速を変かんする【単位量あたりの大きさ14】02確認
- 【03】時速と秒速を変かんする【単位量あたりの大きさ14】03確認
- 【04】時速と秒速を変かんする【単位量あたりの大きさ14】04確認
- 【05】時速と秒速を変かんする【単位量あたりの大きさ14】05定着
- 【06】時速と秒速を変かんする【単位量あたりの大きさ14】06定着
- 【07】時速と秒速を変かんする【単位量あたりの大きさ14】07定着
- 【08】時速と秒速を変かんする【単位量あたりの大きさ14】08定着
- 【09】時速と秒速を変かんする【単位量あたりの大きさ14】09定着
- 【10】時速と秒速を変かんする【単位量あたりの大きさ14】10仕上げ
- 【11】時速と秒速を変かんする【単位量あたりの大きさ14】11仕上げ
- 【12】時速と秒速を変かんする【単位量あたりの大きさ14】12仕上げ
- 【13】時速と秒速を変かんする【単位量あたりの大きさ14】13仕上げ
- 【14】時速と秒速を変かんする【単位量あたりの大きさ14】14仕上げ
- 【15】時速と秒速を変かんする【単位量あたりの大きさ14】15力だめし
- 【16】時速と秒速を変かんする【単位量あたりの大きさ14】16力だめし
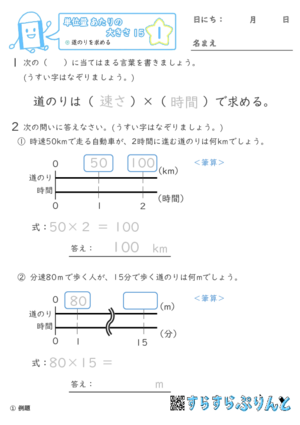
【単位量あたりの大きさ15】道のりを求める

道のりを求める問題を集めた学習プリントです。
道のりは「速さ×時間」で求めます。
『例題』『確認』で公式も書けるようにしましょう。
時間や速さの単位が正しいかどうかのチェックも忘れずに!
『仕上げ』と『力だめし』では、時速・分速・秒速の変換をする問題もまぜてあります。
「【単位量あたりの大きさ15】道のりを求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】道のりを求める【単位量あたりの大きさ15】01例題
- 【02】道のりを求める【単位量あたりの大きさ15】02確認
- 【03】道のりを求める【単位量あたりの大きさ15】03確認
- 【04】道のりを求める【単位量あたりの大きさ15】04確認
- 【05】道のりを求める【単位量あたりの大きさ15】05定着
- 【06】道のりを求める【単位量あたりの大きさ15】06定着
- 【07】道のりを求める【単位量あたりの大きさ15】07定着
- 【08】道のりを求める【単位量あたりの大きさ15】08定着
- 【09】道のりを求める【単位量あたりの大きさ15】09定着
- 【10】道のりを求める【単位量あたりの大きさ15】10仕上げ
- 【11】道のりを求める【単位量あたりの大きさ15】11仕上げ
- 【12】道のりを求める【単位量あたりの大きさ15】12仕上げ
- 【13】道のりを求める【単位量あたりの大きさ15】13仕上げ
- 【14】道のりを求める【単位量あたりの大きさ15】14仕上げ
- 【15】道のりを求める【単位量あたりの大きさ15】15力だめし
- 【16】道のりを求める【単位量あたりの大きさ15】16力だめし
【単位量あたりの大きさ16】道のりを求めて単位を変える

道のりを求めてから、距離の単位変換をする問題を集めた学習プリントです。
例えば、
秒速500mで飛ぶジェット機は15秒で何km進みますか。
という問題では、道のり(m)→道のり(km)の単位変換が必要です。
答えに小数点がつくものも多いですが、単位変換をしましょう。
『仕上げ』と『力だめし』では、単位変換のいらない道のりを求める問題も混ぜてあります。
「【単位量あたりの大きさ16】道のりを求めて単位を変える」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】道のりを求めて単位を変える【単位量あたりの大きさ16】01例題
- 【02】道のりを求めて単位を変える【単位量あたりの大きさ16】02確認
- 【03】道のりを求めて単位を変える【単位量あたりの大きさ16】03確認
- 【04】道のりを求めて単位を変える【単位量あたりの大きさ16】04確認
- 【05】道のりを求めて単位を変える【単位量あたりの大きさ16】05定着
- 【06】道のりを求めて単位を変える【単位量あたりの大きさ16】06定着
- 【07】道のりを求めて単位を変える【単位量あたりの大きさ16】07定着
- 【08】道のりを求めて単位を変える【単位量あたりの大きさ16】08定着
- 【09】道のりを求めて単位を変える【単位量あたりの大きさ16】09定着
- 【10】道のりを求めて単位を変える【単位量あたりの大きさ16】10仕上げ
- 【11】道のりを求めて単位を変える【単位量あたりの大きさ16】11仕上げ
- 【12】道のりを求めて単位を変える【単位量あたりの大きさ16】12仕上げ
- 【13】道のりを求めて単位を変える【単位量あたりの大きさ16】13仕上げ
- 【14】道のりを求めて単位を変える【単位量あたりの大きさ16】14仕上げ
- 【15】道のりを求めて単位を変える【単位量あたりの大きさ16】15力だめし
- 【16】道のりを求めて単位を変える【単位量あたりの大きさ16】16力だめし
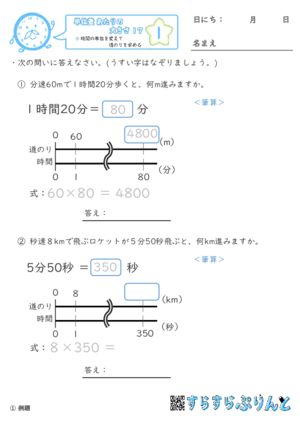
【単位量あたりの大きさ17】時間の単位を変えて道のりを求める

時間の変換をしてから、道のりを求める問題を集めた学習プリントです。
〇時間〇分を「分」に、
〇分〇秒を「秒」に直してから計算します。
問題のバリエーションは、「分速」「秒速」両方出てきます。
分速なら「分」に、秒速なら「秒」に変換しましょう。
『仕上げ』と『力だめし』では、道のりを求めてから距離の単位を変換する問題を混ぜてあります。
「【単位量あたりの大きさ17】時間の単位を変えて道のりを求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】01例題
- 【02】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】02確認
- 【03】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】03確認
- 【04】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】04確認
- 【05】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】05定着
- 【06】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】06定着
- 【07】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】07定着
- 【08】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】08定着
- 【09】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】09定着
- 【10】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】10仕上げ
- 【11】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】11仕上げ
- 【12】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】12仕上げ
- 【13】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】13仕上げ
- 【14】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】14仕上げ
- 【15】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】15力だめし
- 【16】時間の単位を変えて道のりを求める【単位量あたりの大きさ17】16力だめし
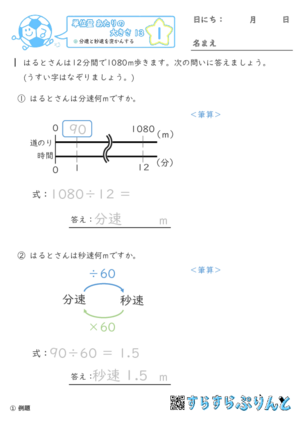
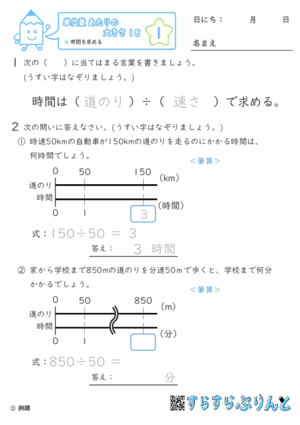
【単位量あたりの大きさ18】時間を求める

速さと道のりから、かかる時間を求める問題を集めた学習プリントです。
「時間」は「道のり÷速さ」で求めます。
『例題』と『確認』で公式も覚えましょう。
「秒速」「分速」「時速」、どの問題も出てきます。
答えの単位に注意しましょう。
『仕上げ』と『力だめし』では、速さを求める問題と道のりを求める問題が混ざっています。
「【単位量あたりの大きさ18】時間を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】時間を求める【単位量あたりの大きさ18】01例題
- 【02】時間を求める【単位量あたりの大きさ18】02確認
- 【03】時間を求める【単位量あたりの大きさ18】03確認
- 【04】時間を求める【単位量あたりの大きさ18】04確認
- 【05】時間を求める【単位量あたりの大きさ18】05定着
- 【06】時間を求める【単位量あたりの大きさ18】06定着
- 【07】時間を求める【単位量あたりの大きさ18】07定着
- 【08】時間を求める【単位量あたりの大きさ18】08定着
- 【09】時間を求める【単位量あたりの大きさ18】09定着
- 【10】時間を求める【単位量あたりの大きさ18】10仕上げ
- 【11】時間を求める【単位量あたりの大きさ18】11仕上げ
- 【12】時間を求める【単位量あたりの大きさ18】12仕上げ
- 【13】時間を求める【単位量あたりの大きさ18】13仕上げ
- 【14】時間を求める【単位量あたりの大きさ18】14仕上げ
- 【15】時間を求める【単位量あたりの大きさ18】15力だめし
- 【16】時間を求める【単位量あたりの大きさ18】16力だめし
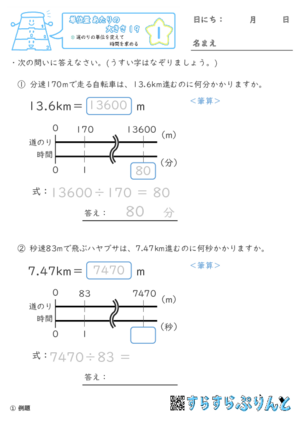
【単位量あたりの大きさ19】道のりの単位を変えて時間を求める

道のりの単位を変換してから、指定の速さで移動したときにかかる時間を求める問題を集めた学習プリントです。
「道のり÷速さ」の公式にあてはめて、かかる時間を計算するときに、道のりと速さの距離の単位はそろっている必要があります。
『定着』までは、単位変換が穴埋め式になっています。
『仕上げ』と『力だめし』では、穴埋めなしで単位変換の計算をしましょう。
また、単位変換なしの時間を求める問題も混ぜてあります。
「【単位量あたりの大きさ19】道のりの単位を変えて時間を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】01例題
- 【02】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】02確認
- 【03】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】03確認
- 【04】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】04確認
- 【05】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】05定着
- 【06】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】06定着
- 【07】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】07定着
- 【08】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】08定着
- 【09】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】09定着
- 【10】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】10仕上げ
- 【11】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】11仕上げ
- 【12】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】12仕上げ
- 【13】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】13仕上げ
- 【14】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】14仕上げ
- 【15】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】15力だめし
- 【16】道のりの単位を変えて時間を求める【単位量あたりの大きさ19】16力だめし
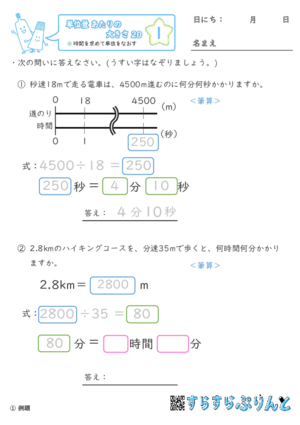
【単位量あたりの大きさ20】時間を求めて単位を直す

速さと道のりからかかる時間を求める問題で、答えを出してから時間の単位変換が必要な問題を集めた学習プリントです。
変換する時間の単位は、
〇分を〇時間〇分にするものと、〇秒を〇分〇秒にするもののどちらもあります。
道のりの単位変換が必要な問題もありますよ!
複数種類の単位変換にも落ち着いて挑戦しましょう。
『定着』までは、単位変換が穴埋め式になっています。
「【単位量あたりの大きさ20】時間を求めて単位を直す」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】時間を求めて単位を直す【単位量あたりの大きさ20】01例題
- 【02】時間を求めて単位を直す【単位量あたりの大きさ20】02確認
- 【03】時間を求めて単位を直す【単位量あたりの大きさ20】03確認
- 【04】時間を求めて単位を直す【単位量あたりの大きさ20】04確認
- 【05】時間を求めて単位を直す【単位量あたりの大きさ20】05定着
- 【06】時間を求めて単位を直す【単位量あたりの大きさ20】06定着
- 【07】時間を求めて単位を直す【単位量あたりの大きさ20】07定着
- 【08】時間を求めて単位を直す【単位量あたりの大きさ20】08定着
- 【09】時間を求めて単位を直す【単位量あたりの大きさ20】09定着
- 【10】時間を求めて単位を直す【単位量あたりの大きさ20】10仕上げ
- 【11】時間を求めて単位を直す【単位量あたりの大きさ20】11仕上げ
- 【12】時間を求めて単位を直す【単位量あたりの大きさ20】12仕上げ
- 【13】時間を求めて単位を直す【単位量あたりの大きさ20】13仕上げ
- 【14】時間を求めて単位を直す【単位量あたりの大きさ20】14仕上げ
- 【15】時間を求めて単位を直す【単位量あたりの大きさ20】15力だめし
- 【16】時間を求めて単位を直す【単位量あたりの大きさ20】16力だめし
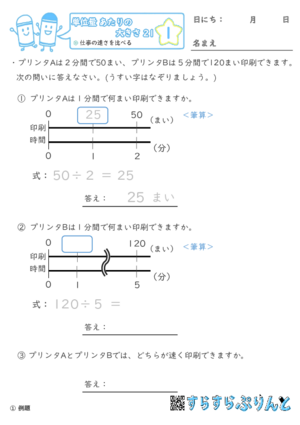
【単位量あたりの大きさ21】仕事の速さを比べる

「仕事の速さ」を比べる問題を集めた学習プリントです。
仕事の速さとは、プリンタの印刷速度や、本を読む速さなど、時間あたりにできる仕事の量のことです。
「仕事量÷時間」で、「仕事の速さ」を出しましょう。
ふたつの仕事の速さを比べる時は、時間あたりの仕事量が多い方が、「速い」といえますね。
『仕上げ』と『力だめし』では、時間を求める速度の問題のうち、答えを出してから時間の単位変換が必要な問題を混ぜてあります。
「【単位量あたりの大きさ21】仕事の速さを比べる」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】仕事の速さを比べる【単位量あたりの大きさ21】01例題
- 【02】仕事の速さを比べる【単位量あたりの大きさ21】02確認
- 【03】仕事の速さを比べる【単位量あたりの大きさ21】03確認
- 【04】仕事の速さを比べる【単位量あたりの大きさ21】04確認
- 【05】仕事の速さを比べる【単位量あたりの大きさ21】05定着
- 【06】仕事の速さを比べる【単位量あたりの大きさ21】06定着
- 【07】仕事の速さを比べる【単位量あたりの大きさ21】07定着
- 【08】仕事の速さを比べる【単位量あたりの大きさ21】08定着
- 【09】仕事の速さを比べる【単位量あたりの大きさ21】09定着
- 【10】仕事の速さを比べる【単位量あたりの大きさ21】10仕上げ
- 【11】仕事の速さを比べる【単位量あたりの大きさ21】11仕上げ
- 【12】仕事の速さを比べる【単位量あたりの大きさ21】12仕上げ
- 【13】仕事の速さを比べる【単位量あたりの大きさ21】13仕上げ
- 【14】仕事の速さを比べる【単位量あたりの大きさ21】14仕上げ
- 【15】仕事の速さを比べる【単位量あたりの大きさ21】15力だめし
- 【16】仕事の速さを比べる【単位量あたりの大きさ21】16力だめし
【単位量あたりの大きさ22】仕事の速さから仕事量を求める

2つの機械の仕事量を比べる問題を集めた学習プリントです。
提示される2つの機械の仕事量は、「〇時間で何個生産」と「×分で何個生産」といったように、時間の単位がそろっていません。
単位を「分」でそろえると、時間あたりの生産量がとても小さい小数になったり、割り切れなかったりします。
1時間あたりいくつ生産できるか? で考えると楽になりますよ。
また、「□時間使ったときに生産できる製品の数」は、1時間あたりに生産できる商品の数を元にして簡単に計算できますね。
「【単位量あたりの大きさ22】仕事の速さから仕事量を求める」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】仕事の速さから仕事量を求める【単位量あたりの大きさ22】01例題
- 【02】仕事の速さから仕事量を求める【単位量あたりの大きさ22】02確認
- 【03】仕事の速さから仕事量を求める【単位量あたりの大きさ22】03確認
- 【04】仕事の速さから仕事量を求める【単位量あたりの大きさ22】04確認
- 【05】仕事の速さから仕事量を求める【単位量あたりの大きさ22】05定着
- 【06】仕事の速さから仕事量を求める【単位量あたりの大きさ22】06定着
- 【07】仕事の速さから仕事量を求める【単位量あたりの大きさ22】07定着
- 【08】仕事の速さから仕事量を求める【単位量あたりの大きさ22】08定着
- 【09】仕事の速さから仕事量を求める【単位量あたりの大きさ22】09定着
- 【10】仕事の速さから仕事量を求める【単位量あたりの大きさ22】10仕上げ
- 【11】仕事の速さから仕事量を求める【単位量あたりの大きさ22】11仕上げ
- 【12】仕事の速さから仕事量を求める【単位量あたりの大きさ22】12仕上げ
- 【13】仕事の速さから仕事量を求める【単位量あたりの大きさ22】13仕上げ
- 【14】仕事の速さから仕事量を求める【単位量あたりの大きさ22】14仕上げ
- 【15】仕事の速さから仕事量を求める【単位量あたりの大きさ22】15力だめし
- 【16】仕事の速さから仕事量を求める【単位量あたりの大きさ22】16力だめし