- 【三角形と角1】辺の長さが等しい三角形の名前プリント数:2
- 【三角形と角2】正三角形と二等辺三角形はどれ?プリント数:4
- 【三角形と角3】コンパスを使った二等辺三角形のかき方プリント数:16
- 【三角形と角4】コンパスを使った正三角形のかき方プリント数:16
- 【三角形と角5】二等辺三角形や正三角形の中の等しい角プリント数:16
- 【三角形と角6】円を使った二等辺三角形のかき方プリント数:4
- 【三角形と角7】円を使った正三角形のかき方プリント数:4
- 【三角形と角8】円と三角形の関係プリント数:16
- 【三角形と角9】三角定規の角プリント数:16
- 【三角形と角10】角を大きいじゅんにならべるプリント数:16
- 【三角形と角11】三角定規で作る三角形の形プリント数:3
- 【三角形と角12】おった紙で作る三角形プリント数:3
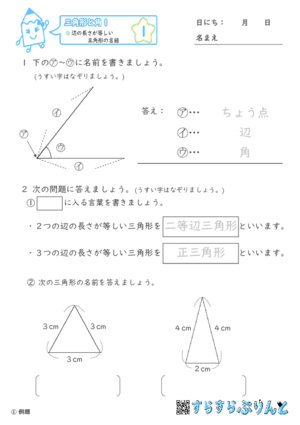
【三角形と角1】辺の長さが等しい三角形の名前

この単元で出てくる大切な言葉をまとめたプリントです。
二等辺三角形は2つの辺の長さが等しく、正三角形は3つの辺の長さが等しいという定義も確認できます。
シンプルな問題なので2枚だけですが、もし練習が足りなければこの2枚を繰り返し使ってください。
「【三角形と角1】辺の長さが等しい三角形の名前」プリント一覧
リンクをクリックするとPDFが表示されます。
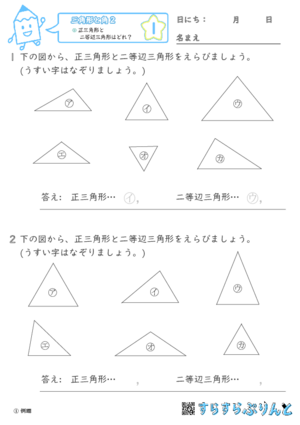
【三角形と角2】正三角形と二等辺三角形はどれ?

いくつかの三角形の中から、正三角形と二等辺三角形を見つける学習プリントです。
※「実際のサイズ」での印刷をおすすめします。
正三角形は3つ(すべて)の辺の長さが等しく、二等辺三角形は2つの辺の長さが等しいです。
見た目でもある程度しぼれますが、定規を当てて確認してみましょう!
複数個答えがあるので、すべての三角形をしっかり見てくださいね。
「【三角形と角2】正三角形と二等辺三角形はどれ?」プリント一覧
リンクをクリックするとPDFが表示されます。
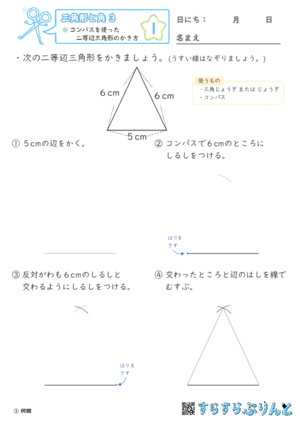
【三角形と角3】コンパスを使った二等辺三角形のかき方

二等辺三角形をコンパスと定規で作図する学習プリントです。
※「実際のサイズ」での印刷をおすすめします。
この作図によって、コンパスは円をかくだけでなく、長さをはかり取ることもできるということもイメージしやすくなりますね!
『①例題』~『④確認』では、作図手順を図つきで解説しています。
『⑤定着』からは問題数を増やしてあるので、たくさん練習して二等辺三角形の作図に慣れましょう。
『⑩仕上げ』~『⑯力だめし』では、いくつかの三角形の中から、正三角形と二等辺三角形を見つける問題も混ぜています。
「【三角形と角3】コンパスを使った二等辺三角形のかき方」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】コンパスを使った二等辺三角形のかき方【三角形と角3】01例題
- 【02】コンパスを使った二等辺三角形のかき方【三角形と角3】02確認
- 【03】コンパスを使った二等辺三角形のかき方【三角形と角3】03確認
- 【04】コンパスを使った二等辺三角形のかき方【三角形と角3】04確認
- 【05】コンパスを使った二等辺三角形のかき方【三角形と角3】05定着
- 【06】コンパスを使った二等辺三角形のかき方【三角形と角3】06定着
- 【07】コンパスを使った二等辺三角形のかき方【三角形と角3】07定着
- 【08】コンパスを使った二等辺三角形のかき方【三角形と角3】08定着
- 【09】コンパスを使った二等辺三角形のかき方【三角形と角3】09定着
- 【10】コンパスを使った二等辺三角形のかき方【三角形と角3】10仕上げ
- 【11】コンパスを使った二等辺三角形のかき方【三角形と角3】11仕上げ
- 【12】コンパスを使った二等辺三角形のかき方【三角形と角3】12仕上げ
- 【13】コンパスを使った二等辺三角形のかき方【三角形と角3】13仕上げ
- 【14】コンパスを使った二等辺三角形のかき方【三角形と角3】14仕上げ
- 【15】コンパスを使った二等辺三角形のかき方【三角形と角3】15力だめし
- 【16】コンパスを使った二等辺三角形のかき方【三角形と角3】16力だめし
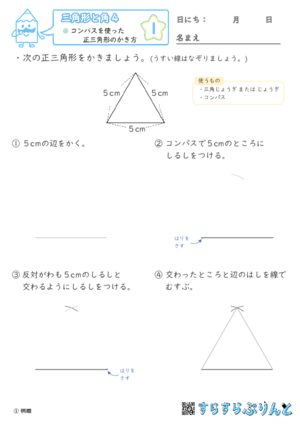
【三角形と角4】コンパスを使った正三角形のかき方

正三角形をコンパスと定規で作図する学習プリントです。
※「実際のサイズ」での印刷をおすすめします。
『①例題』~『④確認』では、作図手順を図つきで解説していますが、基本的な作図の手順は二等辺三角形と変わりません。
『⑤定着』からはたくさん練習できるように問題数を増やしています。
『⑩仕上げ』~『⑯力だめし』では、二等辺三角形の作図も混ぜています。ここで2種類の三角形の作図をマスターしましょう!
「【三角形と角4】コンパスを使った正三角形のかき方」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】コンパスを使った正三角形のかき方【三角形と角4】01例題
- 【02】コンパスを使った正三角形のかき方【三角形と角4】02確認
- 【03】コンパスを使った正三角形のかき方【三角形と角4】03確認
- 【04】コンパスを使った正三角形のかき方【三角形と角4】04確認
- 【05】コンパスを使った正三角形のかき方【三角形と角4】05定着
- 【06】コンパスを使った正三角形のかき方【三角形と角4】06定着
- 【07】コンパスを使った正三角形のかき方【三角形と角4】07定着
- 【08】コンパスを使った正三角形のかき方【三角形と角4】08定着
- 【09】コンパスを使った正三角形のかき方【三角形と角4】09定着
- 【10】コンパスを使った正三角形のかき方【三角形と角4】10仕上げ
- 【11】コンパスを使った正三角形のかき方【三角形と角4】11仕上げ
- 【12】コンパスを使った正三角形のかき方【三角形と角4】12仕上げ
- 【13】コンパスを使った正三角形のかき方【三角形と角4】13仕上げ
- 【14】コンパスを使った正三角形のかき方【三角形と角4】14仕上げ
- 【15】コンパスを使った正三角形のかき方【三角形と角4】15力だめし
- 【16】コンパスを使った正三角形のかき方【三角形と角4】16力だめし
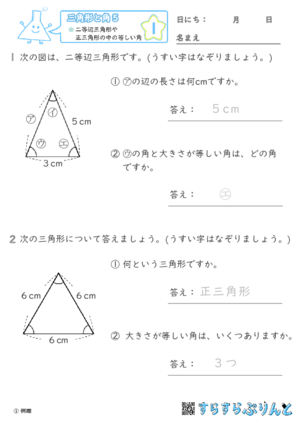
【三角形と角5】二等辺三角形や正三角形の中の等しい角

二等辺三角形と正三角形の等しい辺や等しい角を見つける学習プリントです。
※「実際のサイズ」での印刷をおすすめします。
問題を見ると難しく感じてしまう生徒さんもいるかもしれませんが、パターン化されているので何度も練習すれば大丈夫です! ここで二等辺三角形と正三角形の性質を完ぺきにしておきましょう!
『⑩仕上げ』~『⑯力だめし』では、定規とコンパスで正三角形を作図する問題を混ぜています。
「【三角形と角5】二等辺三角形や正三角形の中の等しい角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】二等辺三角形や正三角形の中の等しい角【三角形と角5】01例題
- 【02】二等辺三角形や正三角形の中の等しい角【三角形と角5】02確認
- 【03】二等辺三角形や正三角形の中の等しい角【三角形と角5】03確認
- 【04】二等辺三角形や正三角形の中の等しい角【三角形と角5】04確認
- 【05】二等辺三角形や正三角形の中の等しい角【三角形と角5】05定着
- 【06】二等辺三角形や正三角形の中の等しい角【三角形と角5】06定着
- 【07】二等辺三角形や正三角形の中の等しい角【三角形と角5】07定着
- 【08】二等辺三角形や正三角形の中の等しい角【三角形と角5】08定着
- 【09】二等辺三角形や正三角形の中の等しい角【三角形と角5】09定着
- 【10】二等辺三角形や正三角形の中の等しい角【三角形と角5】10仕上げ
- 【11】二等辺三角形や正三角形の中の等しい角【三角形と角5】11仕上げ
- 【12】二等辺三角形や正三角形の中の等しい角【三角形と角5】12仕上げ
- 【13】二等辺三角形や正三角形の中の等しい角【三角形と角5】13仕上げ
- 【14】二等辺三角形や正三角形の中の等しい角【三角形と角5】14仕上げ
- 【15】二等辺三角形や正三角形の中の等しい角【三角形と角5】15力だめし
- 【16】二等辺三角形や正三角形の中の等しい角【三角形と角5】16力だめし
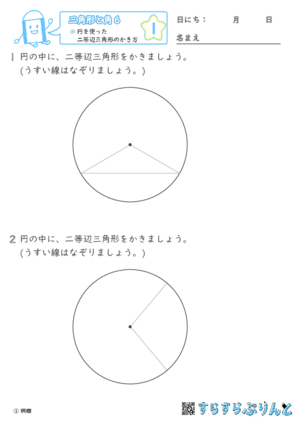
【三角形と角6】円を使った二等辺三角形のかき方

円を使って、二等辺三角形を作図する学習プリントです。
※「実際のサイズ」での印刷をおすすめします。
1つの円では半径はすべて同じ長さであることを利用して二等辺三角形を作図します。
半径をひいた場所次第で、二等辺三角形はいろいろな向きで作れますね!
答えの形だけが正解ではないので、答えには(例)と入れています。半径が同じ長さであることを理解してかけていれば全部正解ですよ!
「【三角形と角6】円を使った二等辺三角形のかき方」プリント一覧
リンクをクリックするとPDFが表示されます。
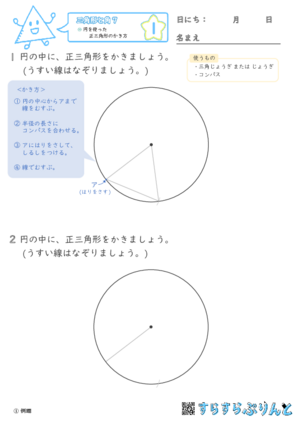
【三角形と角7】円を使った正三角形のかき方

円を使って、正三角形を作図する学習プリントです。
※「実際のサイズ」での印刷をおすすめします。
【三角形と角6】の二等辺三角形のかき方をもとにして、コンパスを使って正三角形を作図します。
円の周りの点を結んだ辺の長さを半径と同じにすれば正三角形をかくことができます。
『①例題』にはかき方の手順を記載しているので参考にしてみてください。
半径をひいた場所次第で、正三角形はいろいろな向きで作れますね!
答えの形だけが正解ではないので、答えには(例)と入れています。半径が同じ長さであることを理解してかけていれば全部正解ですよ!
「【三角形と角7】円を使った正三角形のかき方」プリント一覧
リンクをクリックするとPDFが表示されます。
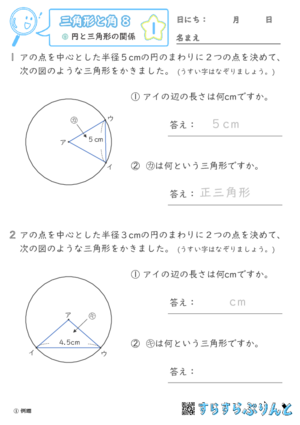
【三角形と角8】円と三角形の関係

円の中にある三角形の名前や辺の長さやを答える学習プリントです。
底辺の長さと半径の長さが同じかどうかで、正三角形と二等辺三角形を区別することができますね!
【三角形と角7】と【三角形と角8】で作図ができていれば、すらすら取り組めますよ!
『⑩仕上げ』~『⑯力だめし』では円を使って、正三角形を作図する問題を混ぜています。
「【三角形と角8】円と三角形の関係」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】円と三角形の関係【三角形と角8】01例題
- 【02】円と三角形の関係【三角形と角8】02確認
- 【03】円と三角形の関係【三角形と角8】03確認
- 【04】円と三角形の関係【三角形と角8】04確認
- 【05】円と三角形の関係【三角形と角8】05定着
- 【06】円と三角形の関係【三角形と角8】06定着
- 【07】円と三角形の関係【三角形と角8】07定着
- 【08】円と三角形の関係【三角形と角8】08定着
- 【09】円と三角形の関係【三角形と角8】09定着
- 【10】円と三角形の関係【三角形と角8】10仕上げ
- 【11】円と三角形の関係【三角形と角8】11仕上げ
- 【12】円と三角形の関係【三角形と角8】12仕上げ
- 【13】円と三角形の関係【三角形と角8】13仕上げ
- 【14】円と三角形の関係【三角形と角8】14仕上げ
- 【15】円と三角形の関係【三角形と角8】15力だめし
- 【16】円と三角形の関係【三角形と角8】16力だめし
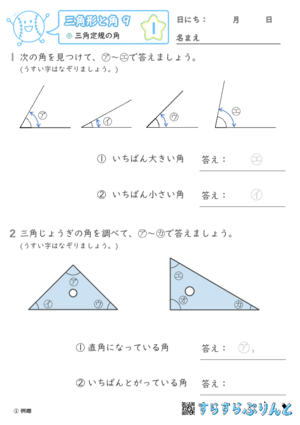
【三角形と角9】三角定規の角

角度の大小を比べる学習プリントです。
角の大きさは角をつくっている辺の開き具合を見ます。
『①例題』~『④確認』では身近な角として三角定規の角を比較する問題も入れています。
『⑩仕上げ』~『⑯力だめし』では、円の中にある三角形の名前や辺の長さやを答える問題を混ぜています。
「【三角形と角9】三角定規の角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】三角定規の角【三角形と角9】01例題
- 【02】三角定規の角【三角形と角9】02確認
- 【03】三角定規の角【三角形と角9】03確認
- 【04】三角定規の角【三角形と角9】04確認
- 【05】三角定規の角【三角形と角9】05定着
- 【06】三角定規の角【三角形と角9】06定着
- 【07】三角定規の角【三角形と角9】07定着
- 【08】三角定規の角【三角形と角9】08定着
- 【09】三角定規の角【三角形と角9】09定着
- 【10】三角定規の角【三角形と角9】10仕上げ
- 【11】三角定規の角【三角形と角9】11仕上げ
- 【12】三角定規の角【三角形と角9】12仕上げ
- 【13】三角定規の角【三角形と角9】13仕上げ
- 【14】三角定規の角【三角形と角9】14仕上げ
- 【15】三角定規の角【三角形と角9】15力だめし
- 【16】三角定規の角【三角形と角9】16力だめし
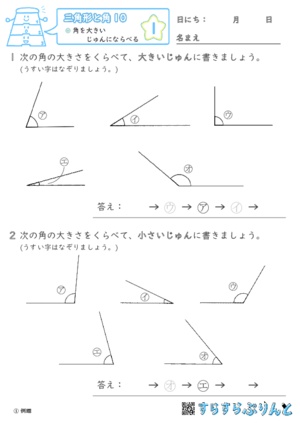
【三角形と角10】角を大きいじゅんにならべる

いくつかある角を、大きい順や、小さい順に並べる学習プリントです。
【三角形と角9】のステップアップ問題なので、【三角形と角9】がすらすらできるようになったら取り組んでみてください。
『⑩仕上げ』~『⑯力だめし』では、いちばん大きい角と、いちばん小さい角を選ぶ問題を混ぜています。
「【三角形と角10】角を大きいじゅんにならべる」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】角を大きいじゅんにならべる【三角形と角10】01例題
- 【02】角を大きいじゅんにならべる【三角形と角10】02確認
- 【03】角を大きいじゅんにならべる【三角形と角10】03確認
- 【04】角を大きいじゅんにならべる【三角形と角10】04確認
- 【05】角を大きいじゅんにならべる【三角形と角10】05定着
- 【06】角を大きいじゅんにならべる【三角形と角10】06定着
- 【07】角を大きいじゅんにならべる【三角形と角10】07定着
- 【08】角を大きいじゅんにならべる【三角形と角10】08定着
- 【09】角を大きいじゅんにならべる【三角形と角10】09定着
- 【10】角を大きいじゅんにならべる【三角形と角10】10仕上げ
- 【11】角を大きいじゅんにならべる【三角形と角10】11仕上げ
- 【12】角を大きいじゅんにならべる【三角形と角10】12仕上げ
- 【13】角を大きいじゅんにならべる【三角形と角10】13仕上げ
- 【14】角を大きいじゅんにならべる【三角形と角10】14仕上げ
- 【15】角を大きいじゅんにならべる【三角形と角10】15力だめし
- 【16】角を大きいじゅんにならべる【三角形と角10】16力だめし
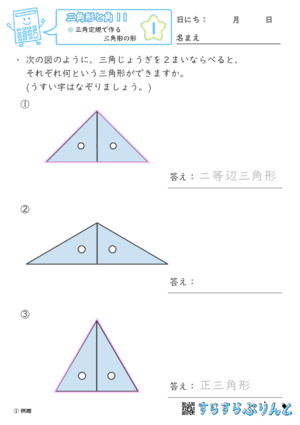
【三角形と角11】三角定規で作る三角形の形

同じ三角定規を2枚組み合わせてできる三角形の名前を答える学習プリントです。
同じ三角定規を同じ長さの辺でくっつけて三角形を作るので、二等辺三角形ができます。
1つだけ正三角形になるパターンがあるので、そこをバッチリおさえましょう!
※直角二等辺三角形を、くっつけた時です。
「【三角形と角11】三角定規で作る三角形の形」プリント一覧
リンクをクリックするとPDFが表示されます。
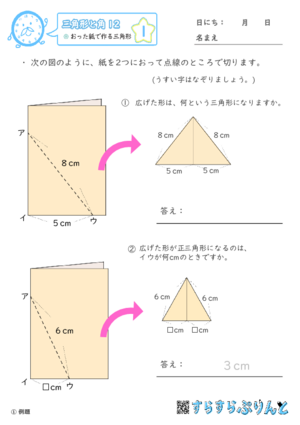
【三角形と角12】おった紙で作る三角形

おり紙を折り、折り目に対して斜めにはさみで切って開いたときにできた三角形についての学習プリントです。
開いたときの長さを思い浮かべながら答えましょう。実際に紙を切ってみるとイメージしやすくなりますよ。
「【三角形と角12】おった紙で作る三角形」プリント一覧
リンクをクリックするとPDFが表示されます。