- 【図形の角1】三角形の内角プリント数:16
- 【図形の角2】正三角形や二等辺三角形の内角プリント数:16
- 【図形の角3】三角形の外角プリント数:16
- 【図形の角4】正三角形や二等辺三角形の外角プリント数:16
- 【図形の角5】四角形の内角プリント数:16
- 【図形の角6】平行四辺形やひし形の内角プリント数:16
- 【図形の角7】四角形の外角プリント数:16
- 【図形の角8】平行四辺形やひし形の外角プリント数:16
- 【図形の角9】色々な多角形の名前プリント数:4
- 【図形の角10】多角形の中の三角形の数プリント数:16
- 【図形の角11】多角形の内角プリント数:16
- 【図形の角12】正多角形の一つの内角プリント数:16
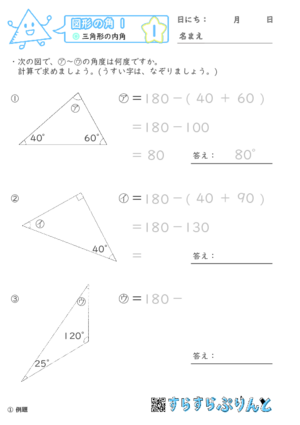
【図形の角1】三角形の内角

三角形の3つの内角のうち、2つの角度が分かっていて、残りの1つの角度を求める問題を集めた学習プリントです。
答えは三角形の内角の和が180°であることを利用して、引き算をして求めることができます。
分かっている角度の和をあらかじめ求めてから、180との差を計算して求めていきます。
計算は簡単ですができればそれだけで終わるのではなく、実際に三角形をハサミで切り抜いて三つの角もバラバラにして並べてみましょう。
一直線に並ぶ!ということを実際に目と手で確認しておきたいです。
三角形の内角についてだけでなく、単純に180度の角とは一直線のことだということも確認しておきたい点です。
「【図形の角1】三角形の内角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】三角形の内角【図形の角1】01例題
- 【02】三角形の内角【図形の角1】02確認
- 【03】三角形の内角【図形の角1】03確認
- 【04】三角形の内角【図形の角1】04確認
- 【05】三角形の内角【図形の角1】05定着
- 【06】三角形の内角【図形の角1】06定着
- 【07】三角形の内角【図形の角1】07定着
- 【08】三角形の内角【図形の角1】08定着
- 【09】三角形の内角【図形の角1】09定着
- 【10】三角形の内角【図形の角1】10仕上げ
- 【11】三角形の内角【図形の角1】11仕上げ
- 【12】三角形の内角【図形の角1】12仕上げ
- 【13】三角形の内角【図形の角1】13仕上げ
- 【14】三角形の内角【図形の角1】14仕上げ
- 【15】三角形の内角【図形の角1】15力だめし
- 【16】三角形の内角【図形の角1】16力だめし
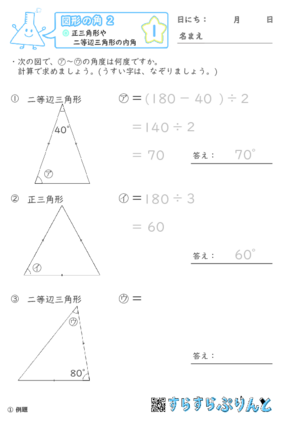
【図形の角2】正三角形や二等辺三角形の内角

正三角形と二等辺三角形の内角を求める問題プリントです。
正三角形の内角は初登場なので計算から求めていきますが、繰り返していくことで覚えてしまいましょう!
二等辺三角形は、頂角がわからないパターンと、底角がわからないパターンの2パターンがあります。
『例題』〜『確認』までの4枚は底角がわからないパターンのみ扱っています。
『定着』から頂角がわからないパターンも扱っていますが、最初はなぞりを入れてあるので気をつけて取り組んでみてほしいです。
さらに定着からは『二等辺三角形』や『正三角形』などの名前も表記しないようになっています。
辺の長さの記号などから読み取らなくてはならなくなるので、小さな違いではありますがつまづきのポイントになる子もいると思います。
『確認』までの4枚を取り組む中で、どういう三角形が二等辺三角形なのかということも確認しておいてあげてください。
「【図形の角2】正三角形や二等辺三角形の内角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】正三角形や二等辺三角形の内角【図形の角2】01例題
- 【02】正三角形や二等辺三角形の内角【図形の角2】02確認
- 【03】正三角形や二等辺三角形の内角【図形の角2】03確認
- 【04】正三角形や二等辺三角形の内角【図形の角2】04確認
- 【05】正三角形や二等辺三角形の内角【図形の角2】05定着
- 【06】正三角形や二等辺三角形の内角【図形の角2】06定着
- 【07】正三角形や二等辺三角形の内角【図形の角2】07定着
- 【08】正三角形や二等辺三角形の内角【図形の角2】08定着
- 【09】正三角形や二等辺三角形の内角【図形の角2】09定着
- 【10】正三角形や二等辺三角形の内角【図形の角2】10仕上げ
- 【11】正三角形や二等辺三角形の内角【図形の角2】11仕上げ
- 【12】正三角形や二等辺三角形の内角【図形の角2】12仕上げ
- 【13】正三角形や二等辺三角形の内角【図形の角2】13仕上げ
- 【14】正三角形や二等辺三角形の内角【図形の角2】14仕上げ
- 【15】正三角形や二等辺三角形の内角【図形の角2】15力だめし
- 【16】正三角形や二等辺三角形の内角【図形の角2】16力だめし
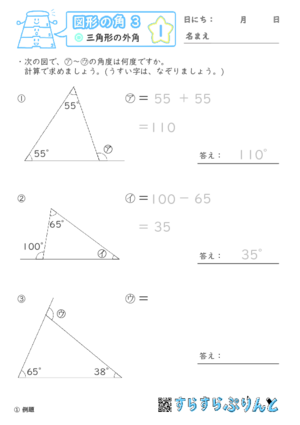
【図形の角3】三角形の外角

三角形の外角を求める問題を集めた学習プリントです。
『三角形の1つの外角は、隣り合わない2つの内角の和に等しい』という、三角形の外角の定理を使って求める問題です。
問題の紙を実際にハサミで切って並べてみると、式の意味が直感的に理解しやすいと思います。
内角の性質(三角形の内角の和が180度になる)を利用して式を作って求めることもできます。
模範解答とは違うやり方にはなりますが、そのやり方で正解していても褒めてあげてください。
もちろん外角の性質を利用したほうが計算ミスなどは減らせるので、模範解答の解き方の方がベターです。
『仕上げ』では内角を求める問題と混ぜてありますので、きちっと問題の見極め・解き方の使い分けをできるように練習していきましょう!
「【図形の角3】三角形の外角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】三角形の外角【図形の角3】01例題
- 【02】三角形の外角【図形の角3】02確認
- 【03】三角形の外角【図形の角3】03確認
- 【04】三角形の外角【図形の角3】04確認
- 【05】三角形の外角【図形の角3】05定着
- 【06】三角形の外角【図形の角3】06定着
- 【07】三角形の外角【図形の角3】07定着
- 【08】三角形の外角【図形の角3】08定着
- 【09】三角形の外角【図形の角3】09定着
- 【10】三角形の外角【図形の角3】10仕上げ
- 【11】三角形の外角【図形の角3】11仕上げ
- 【12】三角形の外角【図形の角3】12仕上げ
- 【13】三角形の外角【図形の角3】13仕上げ
- 【14】三角形の外角【図形の角3】14仕上げ
- 【15】三角形の外角【図形の角3】15力だめし
- 【16】三角形の外角【図形の角3】16力だめし
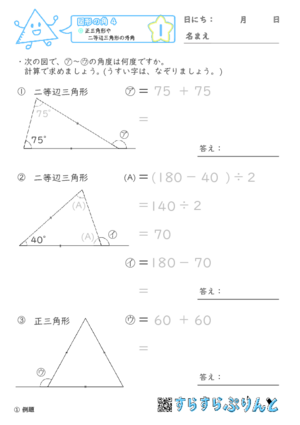
【図形の角4】正三角形や二等辺三角形の外角

三角形の外角を求める問題のうち、二等辺三角形と正三角形を集めた学習プリントです。
前回登場した『三角形の1つの外角は、隣り合わない2つの内角の和に等しい』という、三角形の外角の定理と、二等辺三角形の底角が等しいことや、正三角形の内角は全て60°であることを組みあわせて考えていく問題になります。
正三角形の場合には、外角は決まって120°なので、これは内角が60°となることと合わせて覚えてしまいましょう。
二等辺三角形の場合には、2つの底角が等しいことを利用して、求める外角と隣り合わない2つの内角の和を求めていくことになります。
『定着』以降は、「正三角形」「二等辺三角形」という図形の名前がなくなります。
図形の上の等しい辺マークなどから、その図形がどちらの三角形なのか見分けて解いてください。
『仕上げ』と『力だめし』では、二等辺三角形や正三角形ではない普通の三角形も少し混ぜてあります。
よりいっそう見分ける力が必要になりますので、すらすら解けるようになるまで練習していってください。
「【図形の角4】正三角形や二等辺三角形の外角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】正三角形や二等辺三角形の外角【図形の角4】01例題
- 【02】正三角形や二等辺三角形の外角【図形の角4】02確認
- 【03】正三角形や二等辺三角形の外角【図形の角4】03確認
- 【04】正三角形や二等辺三角形の外角【図形の角4】04確認
- 【05】正三角形や二等辺三角形の外角【図形の角4】05定着
- 【06】正三角形や二等辺三角形の外角【図形の角4】06定着
- 【07】正三角形や二等辺三角形の外角【図形の角4】07定着
- 【08】正三角形や二等辺三角形の外角【図形の角4】08定着
- 【09】正三角形や二等辺三角形の外角【図形の角4】09定着
- 【10】正三角形や二等辺三角形の外角【図形の角4】10仕上げ
- 【11】正三角形や二等辺三角形の外角【図形の角4】11仕上げ
- 【12】正三角形や二等辺三角形の外角【図形の角4】12仕上げ
- 【13】正三角形や二等辺三角形の外角【図形の角4】13仕上げ
- 【14】正三角形や二等辺三角形の外角【図形の角4】14仕上げ
- 【15】正三角形や二等辺三角形の外角【図形の角4】15力だめし
- 【16】正三角形や二等辺三角形の外角【図形の角4】16力だめし
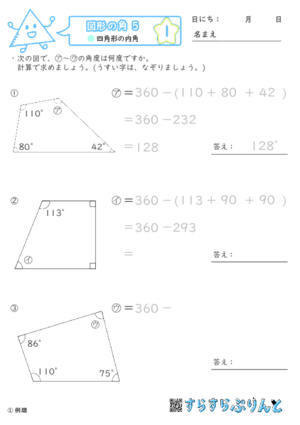
【図形の角5】四角形の内角

四角形の内角を求める問題を集めた学習プリントです。
四角形の内角の和は360°になることから、四つの内角のうちわからない1つの内角を求めていきます。
三角形の内角の学習の時のように、紙のプリントなので一度切って並べてぴったり360°になることを確認してみてください。
『仕上げ』と『力だめし』では、三角形の内角や外角の問題も混ぜてあります。
正三角形や、二等辺三角形も登場させているので、バッチリ復習していきましょう!
「【図形の角5】四角形の内角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】四角形の内角【図形の角5】01例題
- 【02】四角形の内角【図形の角5】02確認
- 【03】四角形の内角【図形の角5】03確認
- 【04】四角形の内角【図形の角5】04確認
- 【05】四角形の内角【図形の角5】05定着
- 【06】四角形の内角【図形の角5】06定着
- 【07】四角形の内角【図形の角5】07定着
- 【08】四角形の内角【図形の角5】08定着
- 【09】四角形の内角【図形の角5】09定着
- 【10】四角形の内角【図形の角5】10仕上げ
- 【11】四角形の内角【図形の角5】11仕上げ
- 【12】四角形の内角【図形の角5】12仕上げ
- 【13】四角形の内角【図形の角5】13仕上げ
- 【14】四角形の内角【図形の角5】14仕上げ
- 【15】四角形の内角【図形の角5】15力だめし
- 【16】四角形の内角【図形の角5】16力だめし
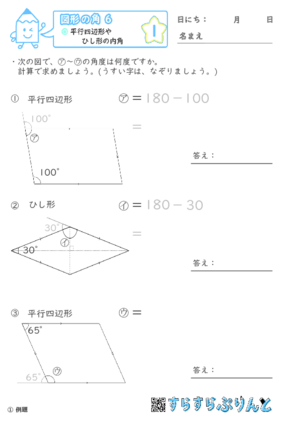
【図形の角6】平行四辺形やひし形の内角

平行四辺形やひし形の内角や外角を求める問題を集めた学習プリントです。
平行四辺形やひし形は、対角が等しい性質があります。
また、隣り合う内角を足すと180°になります。
これらを利用して、一つの内角から他の内角や外角を求めていきます。
隣り合う内角の和が180°になるということは、ある内角とその隣の角の外角が等しくなるのですが、それを図にヒントとして盛り込みました。
『仕上げ』と『力だめし』では、そのほかの四角形の内角や外角を求める問題も混ぜてあります。
等しい長さを表す記号などから、それぞれがどんな四角形なのかを見極めて解き方を使い分けられるように練習していきましょう。
「【図形の角6】平行四辺形やひし形の内角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】平行四辺形やひし形の内角【図形の角6】01例題
- 【02】平行四辺形やひし形の内角【図形の角6】02確認
- 【03】平行四辺形やひし形の内角【図形の角6】03確認
- 【04】平行四辺形やひし形の内角【図形の角6】04確認
- 【05】平行四辺形やひし形の内角【図形の角6】05定着
- 【06】平行四辺形やひし形の内角【図形の角6】06定着
- 【07】平行四辺形やひし形の内角【図形の角6】07定着
- 【08】平行四辺形やひし形の内角【図形の角6】08定着
- 【09】平行四辺形やひし形の内角【図形の角6】09定着
- 【10】平行四辺形やひし形の内角【図形の角6】10仕上げ
- 【11】平行四辺形やひし形の内角【図形の角6】11仕上げ
- 【12】平行四辺形やひし形の内角【図形の角6】12仕上げ
- 【13】平行四辺形やひし形の内角【図形の角6】13仕上げ
- 【14】平行四辺形やひし形の内角【図形の角6】14仕上げ
- 【15】平行四辺形やひし形の内角【図形の角6】15力だめし
- 【16】平行四辺形やひし形の内角【図形の角6】16力だめし
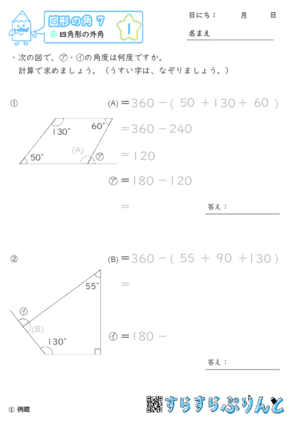
【図形の角7】四角形の外角

いろいろな形の四角形の内角や外角を求める問題を集めた学習プリントです。
四角形の内角の和が360°であることを利用して、ひとつだけ角度のわからない内角を、360° −(その他の3つの角度の合計)で求めることができます。
求めた内角の隣の外角は、180° −(求めた内角の角度)で求めることができます。
このプロセスがわかるプリントを繰り返すことで、四角形の外角を求める問題の解き方で迷わなくなるので、『例題』『確認』『定着』でたっぷりとこの形式の問題を用意しました。
『仕上げ』と『力だめし』では少し問題の数を増やし、平行四辺形やひし形の問題も混ぜてあります。
どの四角形が出てきても、内角を四角形の性質から求めることと、内角を求めてから外角を求めることは変わりません。
平行四辺形やひし形の場合は、隣り合う外角と内角・隣り合う内角同士がいずれも180°になるということから求める方法もあり、気づくことができればこちらの方が早くとけます。
解き方を理解してどんな四角形が出ても内角や外角を求められるようになりましょう!
「【図形の角7】四角形の外角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】四角形の外角【図形の角7】01例題
- 【02】四角形の外角【図形の角7】02確認
- 【03】四角形の外角【図形の角7】03確認
- 【04】四角形の外角【図形の角7】04確認
- 【05】四角形の外角【図形の角7】05定着
- 【06】四角形の外角【図形の角7】06定着
- 【07】四角形の外角【図形の角7】07定着
- 【08】四角形の外角【図形の角7】08定着
- 【09】四角形の外角【図形の角7】09定着
- 【10】四角形の外角【図形の角7】10仕上げ
- 【11】四角形の外角【図形の角7】11仕上げ
- 【12】四角形の外角【図形の角7】12仕上げ
- 【13】四角形の外角【図形の角7】13仕上げ
- 【14】四角形の外角【図形の角7】14仕上げ
- 【15】四角形の外角【図形の角7】15力だめし
- 【16】四角形の外角【図形の角7】16力だめし
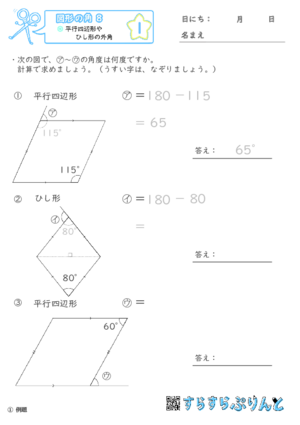
【図形の角8】平行四辺形やひし形の外角

平行四辺形やひし形の内角や外角を求める問題を集めた学習プリントです。
平行四辺形・ひし形の角度の性質
- 2組の対角(向かい合った内角)がそれぞれ等しい
- 隣り合った内角の和は180°
慣れてきたら、「外角を聞かれたら、隣の角の内角と同じだな!」と気付けると良いですね。
『仕上げ』と『力だめし』では普通の四角形も出てきます。
四角形の内角の和が360°であることなども思い出しながら、どんな四角形がきても大丈夫なように練習していってください。
「【図形の角8】平行四辺形やひし形の外角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】平行四辺形やひし形の外角【図形の角8】01例題
- 【02】平行四辺形やひし形の外角【図形の角8】02確認
- 【03】平行四辺形やひし形の外角【図形の角8】03確認
- 【04】平行四辺形やひし形の外角【図形の角8】04確認
- 【05】平行四辺形やひし形の外角 【図形の角8】05定着
- 【06】平行四辺形やひし形の外角【図形の角8】06定着
- 【07】平行四辺形やひし形の外角【図形の角8】07定着
- 【08】平行四辺形やひし形の外角【図形の角8】08定着
- 【09】平行四辺形やひし形の外角【図形の角8】09定着
- 【10】平行四辺形やひし形の外角【図形の角8】10仕上げ
- 【11】平行四辺形やひし形の外角【図形の角8】11仕上げ
- 【12】平行四辺形やひし形の外角【図形の角8】12仕上げ
- 【13】平行四辺形やひし形の外角【図形の角8】13仕上げ
- 【14】平行四辺形やひし形の外角【図形の角8】14仕上げ
- 【15】平行四辺形やひし形の外角【図形の角8】15力だめし
- 【16】平行四辺形やひし形の外角【図形の角8】16力だめし
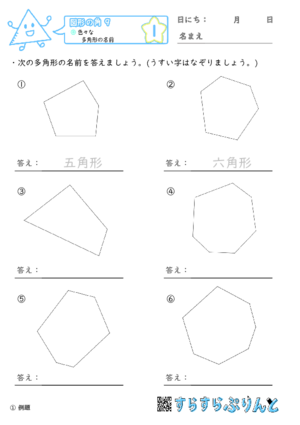
【図形の角9】色々な多角形の名前

様々な多角形の名前を答える問題を集めた学習プリントです。
三角形から九角形までありますが、長方形・正方形・正三角形といった特殊な形は含んでいません。
多角形の名前を答えるだけのとっても簡単な内容なので、枚数は4枚のみです。
とはいえ、図形が苦手なたくさんの子をみていると、意外と多角形の名前とそれが表す図形のイメージが結びついていない子が多くいます。
この後続く多角形の内角の大事な導入になりますので、ちゃんと取り組ませてみてください。
「【図形の角9】色々な多角形の名前」プリント一覧
リンクをクリックするとPDFが表示されます。
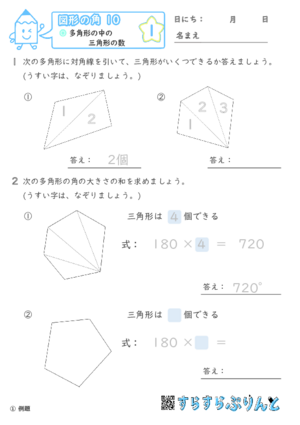
【図形の角10】多角形の中の三角形の数

色々な多角形の内角の和を求めるために、多角形を三角形に分割したときの個数から考える問題を集めた学習プリントです。
多角形の内角の和は、その多角形を三角形に分割したときの個数から計算することができます。
・四角形なら、2個
・五角形なら、3個
・六角形なら、4個 ……
三角形の内角の和が180°であることから、180°と三角形の個数との積で求めます。
このプリントでは、まず多角形を三角形に分割してその個数を数えるところから解説しています。
n角形の内角の和の求め方は、『内角の和 = 180° ×( n - 2 )』という公式になるわけですが、公式だけ覚えても後で思い出しにくく、結局テストなどの必要な場面で間違えてしまうということが多々あります。
求め方の手順だけ丸暗記するのではなく、『多角形を三角形に分けているだけだ』という仕組みを押さえていってほしいです!
『仕上げ』と『力だめし』では、四角形(ひし形・平行四辺形も含む)の外角を求める問題も混ぜてあります。
「【図形の角10】多角形の中の三角形の数」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】多角形の中の三角形の数【図形の角10】01例題
- 【02】多角形の中の三角形の数【図形の角10】02確認
- 【03】多角形の中の三角形の数【図形の角10】03確認
- 【04】多角形の中の三角形の数【図形の角10】04確認
- 【05】多角形の中の三角形の数【図形の角10】05定着
- 【06】多角形の中の三角形の数【図形の角10】06定着
- 【07】多角形の中の三角形の数【図形の角10】07定着
- 【08】多角形の中の三角形の数【図形の角10】08定着
- 【09】多角形の中の三角形の数【図形の角10】09定着
- 【10】多角形の中の三角形の数【図形の角10】10仕上げ
- 【11】多角形の中の三角形の数【図形の角10】11仕上げ
- 【12】多角形の中の三角形の数【図形の角10】12仕上げ
- 【13】多角形の中の三角形の数【図形の角10】13仕上げ
- 【14】多角形の中の三角形の数【図形の角10】14仕上げ
- 【15】多角形の中の三角形の数【図形の角10】15力だめし
- 【16】多角形の中の三角形の数【図形の角10】16力だめし
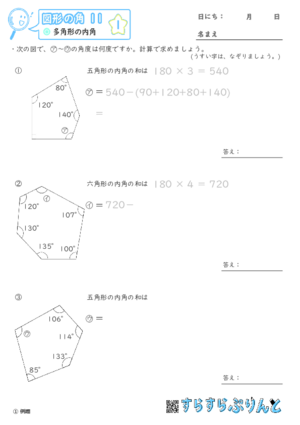
【図形の角11】多角形の内角

多角形について、1つだけ角度のわからない内角を求める問題の学習プリントです。
前回のプリントで登場した、多角形の内角の和を利用します。
(多角形の内角の和 = 180° × 分割できる三角形の数)
求め方の手順
- 求める角以外の、多角形の内角を全て足す
- 公式を利用して、多角形の内角の和を求める
- 2で求めた多角形の内角の和から、1で求めたその他の内角の合計を引く
意外と生徒がつまづきやすい点が、90°の場合だけ角度ではなく直角記号で表しているということです。
『直角記号は90°を表しているんだよ』ということは確認してあげてから取り組ませてみてください。
『仕上げ』と『力だめし』では、多角形の内角の和を求める問題も混ぜてあります。今回の問題の前提になる問題です。
解き方はばっちりだと思いますが、別の問題と混ざっているときでもすらすら解けるように、練習してみてください。
「【図形の角11】多角形の内角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】多角形の内角【図形の角11】01例題
- 【02】多角形の内角【図形の角11】02確認
- 【03】多角形の内角【図形の角11】03確認
- 【04】多角形の内角【図形の角11】04確認
- 【05】多角形の内角【図形の角11】05定着
- 【06】多角形の内角【図形の角11】06定着
- 【07】多角形の内角【図形の角11】07定着
- 【08】多角形の内角【図形の角11】08定着
- 【09】多角形の内角【図形の角11】09定着
- 【10】多角形の内角【図形の角11】10仕上げ
- 【11】多角形の内角【図形の角11】11仕上げ
- 【12】多角形の内角【図形の角11】12仕上げ
- 【13】多角形の内角【図形の角11】13仕上げ
- 【14】多角形の内角【図形の角11】14仕上げ
- 【15】多角形の内角【図形の角11】15力だめし
- 【16】多角形の内角【図形の角11】16力だめし
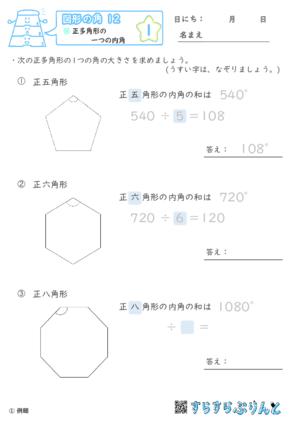
【図形の角12】正多角形の一つの内角

正多角形の内角を求める問題を集めた学習プリントです。
これまでのプリントで、多角形の内角の和を求められるようになりました。
正多角形の場合も同じように、
三角形に分割してた個数×180
で、内角の和が分かります。
正多角形は全ての角の大きさが同じなため、
内角の和÷角の個数
で求めることができます。
この角の個数が、正〇角形に当てはまる数になっていることも、このプリントではわかりやすく習熟できます。
正多角形のひとつの内角を、覚えている生徒さんもいるかと思います。
それもとても良いことですが、ゼロからの求め方も忘れないように、一度はやり方も確認してみましょう。
『仕上げ』と『力だめし』では、多角形のうち一つの内角だけ分からないものを求める問題を混ぜてあります。
「【図形の角12】正多角形の一つの内角」プリント一覧
リンクをクリックするとPDFが表示されます。
- 【01】正多角形の一つの内角【図形の角12】01例題
- 【02】正多角形の一つの内角【図形の角12】02確認
- 【03】正多角形の一つの内角【図形の角12】03確認
- 【04】正多角形の一つの内角【図形の角12】04確認
- 【05】正多角形の一つの内角【図形の角12】05定着
- 【06】正多角形の一つの内角【図形の角12】06定着
- 【07】正多角形の一つの内角【図形の角12】07定着
- 【08】正多角形の一つの内角【図形の角12】08定着
- 【09】正多角形の一つの内角【図形の角12】09定着
- 【10】正多角形の一つの内角【図形の角12】10仕上げ
- 【11】正多角形の一つの内角【図形の角12】11仕上げ
- 【12】正多角形の一つの内角【図形の角12】12仕上げ
- 【13】正多角形の一つの内角【図形の角12】13仕上げ
- 【14】正多角形の一つの内角【図形の角12】14仕上げ
- 【15】正多角形の一つの内角【図形の角12】15力だめし
- 【16】正多角形の一つの内角【図形の角12】16力だめし